Wprowadzamy oznaczenia:

a — krawędź podstawy,

x — krótsza przekątna podstawy,

h —wysokość ostrosłupa.

Z warunków zadania otrzymujemy

x + h = 9, stąd h = 9 – x

Zauważmy, że 0<x<9

Ponieważ x = a√3 , zatem

h = 9 – a√3 , gdzie 0<a<3√3

Objętość tego ostrosłupa wyraża się wzorem

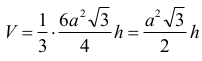
Objętość ostrosłupa przedstawiamy jako funkcję:

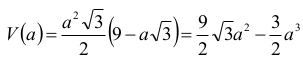
Określamy dziedzinę funkcji:

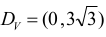
Rozważmy funkcję

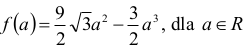
Wyznaczamy pierwszą pochodną:

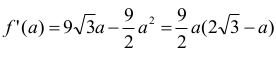
ƒ'(a) = 0 dla a = 0 lub a = 2√3

Analizujemy znak pierwszej pochodnej:

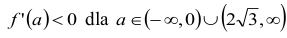
i

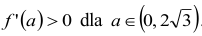
Uwzględniając założenie 0<a<3√3 dla funkcji V opisującej objętość ostrosłupa, otrzymujemy, że dla a = 2√3 spełniony jest warunek konieczny i dostateczny istnienia ekstremum.

Z monotoniczności funkcji, która została zobrazowana w tabeli powyżej, wynika, że wartość funkcji V dla argumentu a = 2√3 jest wartością największą tej funkcji.

Dla a = 2√3  otrzymujemy

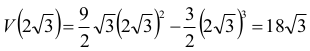
Zatem objętość tego ostrosłupa osiąga największą wartość równą 18√3, gdy krawędź podstawy jest równa a = 2√3