Skorzystamy z własności pochodnej wielomianu: jeśli w danym przedziale otwartym pochodna jest dodatnia, to funkcja jest w przedziale domkniętym rosnąca.

Obliczamy pochodną funkcji ƒ:

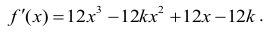
Rozwiązujemy nierówność

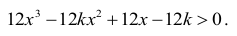
Równoważnie,

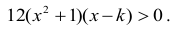
Nierówność jest zatem spełniona wtedy i tylko wtedy, gdy x > k, zatem funkcja ƒ jest rosnąca w przedziale ⟨k,+∞) i nie jest rosnąca w żadnym przedziale postaci ⟨a,+∞) dla a < k. Stąd odpowiedź: k = 2 .