Wobec faktu, że funkcja wymierna ma pochodną w każdym punkcie swojej dziedziny (którą tu jest zbiór wszystkich liczb rzeczywistych), wartości najmniejszej lub największej w przedziale należy szukać w punktach z tego przedziału, w których pochodna jest równa 0, lub na krańcach przedziału.

Obliczamy pochodną funkcji ƒ :

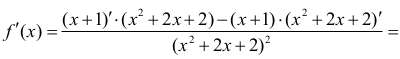
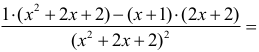
Tak więc ƒ'(x) = 0 wtedy i tylko wtedy, gdy x² + 2x = 0.

To ostatnie równanie ma dwa rozwiązania: 0 oraz -2 i oba należą do przedziału ⟨–3,1⟩.

Największą lub najmniejszą wartość funkcja ƒ może zatem przyjąć tylko w punktach: –3, –2, 0 lub 1.

Możemy teraz podstawić te argumenty do wzoru funkcji i porównać otrzymane wyniki:

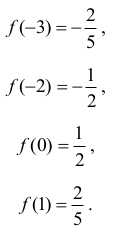
Stwierdzamy przez porównanie, że najmniejszą wartością funkcji ƒ w przedziale ⟨–3,1⟩ jest –½, , największą zaś ½.