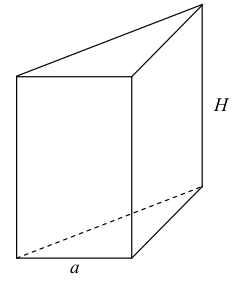
Wprowadzamy oznaczenia:

a — krawędź podstawy graniastosłupa,

H — wysokość graniastosłupa.

Z warunków zadania mamy:

6a + 3H = 12

stąd H = 4 – 2a

Zapisujemy wzór na objętość graniastosłupa:

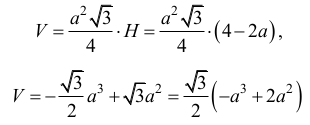
dla 0<a<2.

Rozważamy funkcję ƒ(a) = –a³ + 2a² określoną dla każdej liczby rzeczywistej a.

Obliczamy pochodną tej funkcji:

ƒ'(a) = –3a² + 4a

Znajdujemy miejsca zerowe pochodnej:

–a(3a – 4) = 0

stąd a₁ = 0, a₂ = ⁴⁄₃

Ponadto:

ƒ'(a) > 0 dla a należącego do przedziału (0,⁴⁄₃)

ƒ'(a) < 0 w każdym z przedziałów (–∞,0) oraz (⁴⁄₃,+∞)

Zatem funkcja ƒ jest rosnąca w przedziale ⟨0,⁴⁄₃⟩ i malejąca w każdym z przedziałów (–∞,0⟩ oraz ⟨⁴⁄₃,+∞).

Ponieważ V(a) = ^√3⁄₂ · ƒ(a) dla 0<a<2, to w przedziale (0,2) funkcja V(a) ma ekstremum w tym samym punkcie, w którym ma je funkcja ƒ(a).

Stąd oraz z monotoniczności (współczynnik ^√3⁄₂  jest liczbą dodatnią) wynika, że w punkcie a = ⁴⁄₃ funkcja V przyjmuje największą wartość.

Szukane długości boków graniastosłupa są więc równe:

a = ⁴⁄₃

H = 4 – 2·⁴⁄₃ = ⁴⁄₃.

Objętość graniastosłupa jest równa

V = ^16√3⁄₂₇