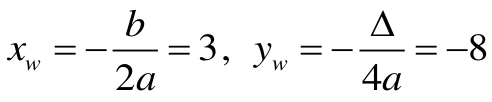
y = x² – 6x +1. 

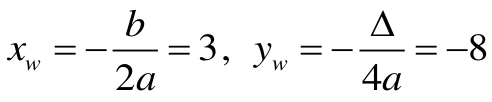
Ponieważ parabola ma ramiona skierowane do góry, to w przedziale (–∞ ,3⟩ dana funkcja maleje. Zatem maleje także na zawartym w nim przedziale ⟨0,1⟩. 

Wobec tego najmniejszą wartość przyjmie ona w prawym końcu, czyli dla x = 1. 

Tą wartością jest 

y = 1² – 6 · 1 +1 = –4.