Trójkąty ABD, ACD i ABC są równoramienne, więc
|∢DAB| = |∢BAD| = α, 

|∢CAD| = |∢ACD| = β

oraz 

|∢CAB| = |∢CBA| = a + β

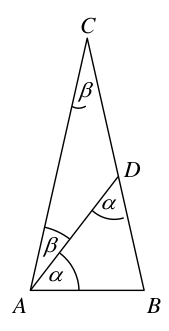
Suma miar kątów trójkąta ACD jest równa 180°, więc
|∢ADC| = 180° – 2β

Z drugiej strony |∢ADC| = 180° – |∢ADB|, 

czyli

180° – 2β = 180°– α

Stąd a = 2β

Suma miar kątów trójkąta ABC jest równa 180°, więc 

2 (α + β) + β = 180°, czyli 

2(2β + β) + β = 180°

Stąd 7β = 180°

Zatem |∢ADC| = 180° – 2β = 7β – 2β = 5β = 5 · |∢ACD|

To kończy dowód.

Rozwiązanie II

Oznaczmy kąty α i β jak w poprzednim rozwiązaniu.
Ponieważ kąt ADB jest kątem zewnętrznym trójkąta ADC, więc a = 2β

Również kąt ADC jest kątem zewnętrznym trójkąta ABD, więc 

|∢ADC| = α + α + β = 2α + β = 4β + β = 5β = 5 · |∢ACD|

co kończy dowód.