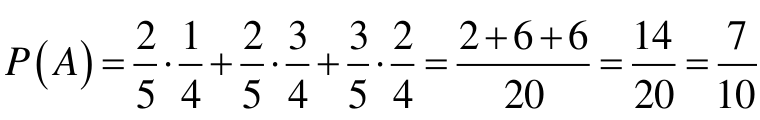Odpowiedź:
Rozwiązanie I (model klasyczny)
Oznaczmy przez w1, w2 losy wygrywające, a przez p1, p2, p3 losy puste. Wszystkie wyniki
losowania dwóch losów bez zwracania możemy przedstawić w tabeli: wynik pierwszego
losowania wyznacza wiersz, a wynik drugiego losowania – kolumnę, w przecięciu których
leży pole, odpowiadające tej parze losowań. Pola położone na przekątnej odrzucamy, gdyż
odpowiadałyby one wylosowaniu dwukrotnie tego samego losu, a to jest niemożliwe, gdyż
losujemy bez zwracania.
Niech A oznacza zdarzenie polegające na wylosowaniu dwóch losów, wśród których co
najmniej jeden jest wygrywający. Zdarzenia elementarne sprzyjające zdarzeniu A zaznaczamy
w tabeli krzyżykiem (x).
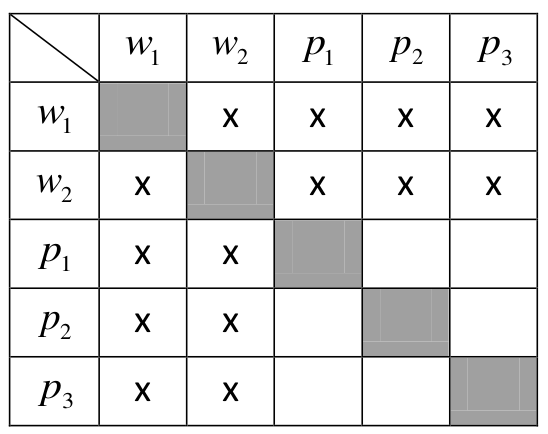
Mamy więc 20 wszystkich zdarzeń elementarnych, czyli |Ω| = 20 , oraz 14 zdarzeń elementarnych sprzyjających zdarzeniu A, czyli |A| = 14.
Prawdopodobieństwo zdarzenia A jest zatem równe
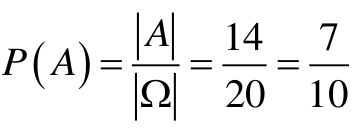
Rozwiązanie II (metoda drzewa)
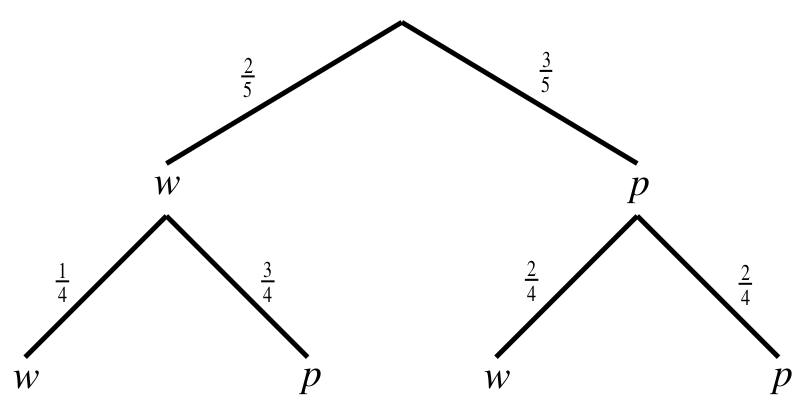
Losowanie z pojemnika kolejno dwóch losów bez zwracania możemy zilustrować za pomocą
drzewa, gdzie w oznacza wylosowanie losu wygrywającego, a p – losu pustego. Pogrubione
gałęzie drzewa odpowiadają zdarzeniu A polegającemu na wylosowaniu dwóch losów, wśród
których co najmniej jeden jest wygrywający. Na odcinkach drzewa zostały zapisane
odpowiednie prawdopodobieństwa.
Zatem prawdopodobieństwo zdarzenia A jest równe