Odpowiedź:
Rozwiązanie I
Ponieważ obie strony danej nierówności
są dodatnie, możemy je podnieść do kwadratu. Otrzymujemy kolejno:
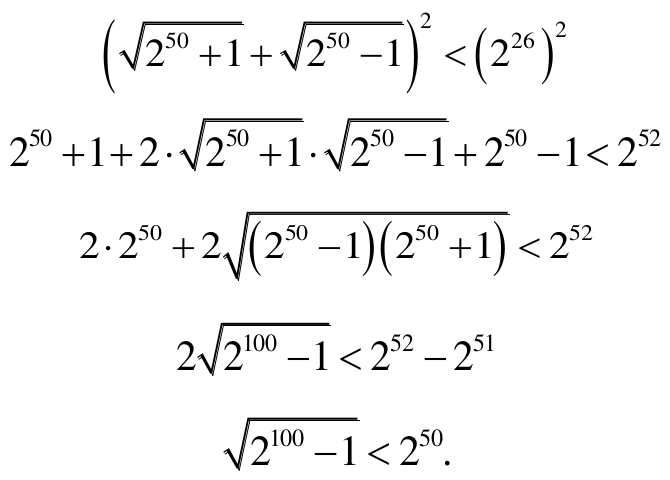
Obie strony tej nierówności są także dodatnie, więc podnosząc je do kwadratu otrzymujemy
2100 – 1 < 2100
Otrzymana nierówność jest oczywiście prawdziwa, a zatem dana w zadaniu nierówność jest również prawdziwa, co kończy dowód.
Rozwiązanie II
Oznaczmy
Zauważmy, że dla dowolnych liczb a, b, takich, że a ≠ b ,
mamy (a – b)2 > 0 ,
skąd a2 + b2 > 2ab.
Wobec tego
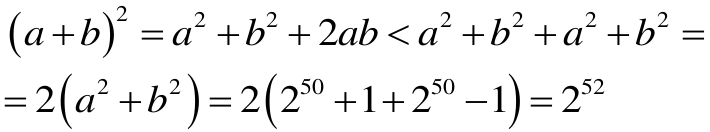
Stąd
co kończy dowód.