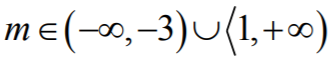Odpowiedź:
Funkcja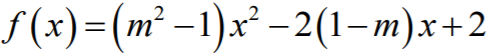 w zależności od parametru m jest liniowa lub
kwadratowa. Rozważmy dwa przypadki:
w zależności od parametru m jest liniowa lub
kwadratowa. Rozważmy dwa przypadki:
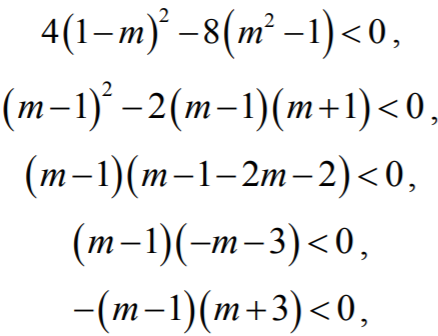
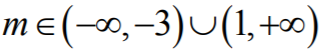
1. Gdy
m2 – 1 = 0, to funkcja ƒ jest liniowa.
- dla m = –1 funkcja ma wzór ƒ(x) = –4x + 2, więc m = –1 nie spełnia warunków zadania.
- dla m = 1 funkcja ma wzór ƒ(x) = 2, więc m = 1 spełnia warunki zadania.
2. Gdy m2 – 1 ≠ 0, to funkcja ƒ jest kwadratowa. Funkcja kwadratowa przyjmuje wartości
dodatnie dla każdej liczby rzeczywistej x, gdy parabola będąca jej wykresem leży
w całości nad osią Ox. Funkcja 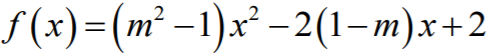 ma tę własność, kiedy
zachodzą warunki:
ma tę własność, kiedy
zachodzą warunki:
- m2 – 1 > 0
- Δ < 0
Pierwszy warunek jest spełniony dla
m ∈ (–∞, –1)∪(1, +∞)
Warunek Δ < 0
jest spełniony, gdy:
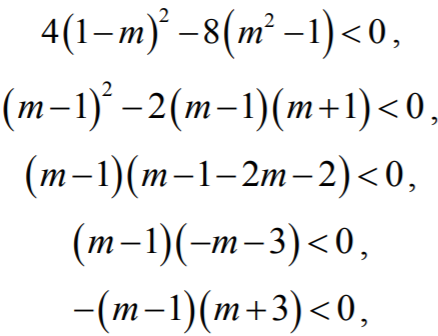
Zatem funkcja kwadratowa przyjmuje wartości dodatnie dla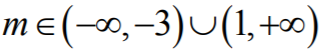
Uwzględniając oba przypadki, otrzymujemy