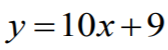
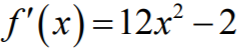
Wyznaczamy pochodną funkcji ƒ:

Zauważamy, że dla x = –1 oraz dla x = 1 pochodna funkcji ƒ ma wartość 10 i równa się współczynnikowi kierunkowemu prostej l.

Obliczamy wartość funkcji ƒ w punkcie x = –1:

ƒ(–1) = –1

oraz w punkcie x = 1:

ƒ(1) = 3

Punkt o współrzędnych (–1, –1) leży na prostej l, natomiast punkt o współrzędnych (1, 3) nie leży na tej prostej.

Zatem prosta o równaniu 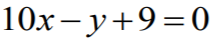 jest styczna do wykresu funkcji ƒ, co kończy dowód.