Odpowiedź:
Niech
x = |AO| = |BO| = |CO| (zobacz rysunek) oznacza promień okręgu opisanego na
podstawie ostrosłupa oraz
h = |SO| oznacza wysokość tego ostrosłupa. Wówczas
Wysokość AD w trójkącie ABC jest równa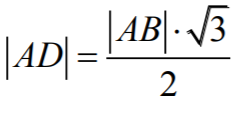
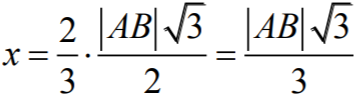
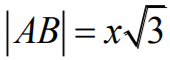
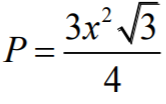
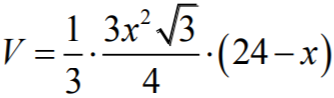
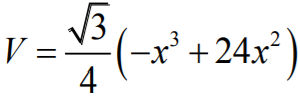
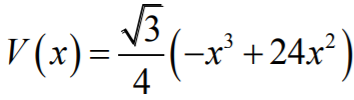
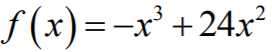
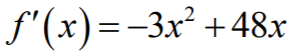
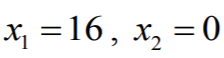
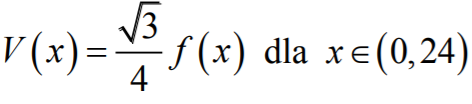
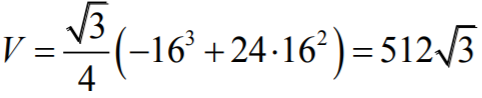
x + h = 24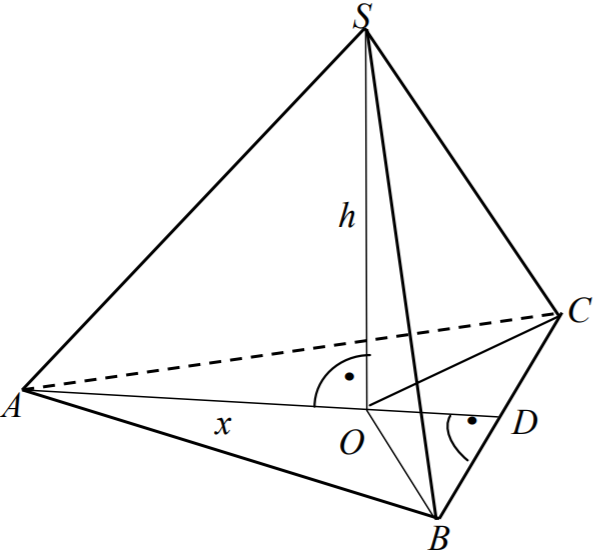

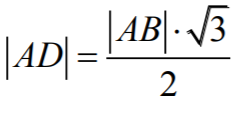
Zatem promień x okręgu
opisanego na trójkącie ABC (podstawie ostrosłupa) jest równy:
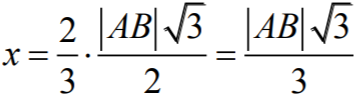
stąd
Wyznaczamy pole podstawy ostrosłupa:
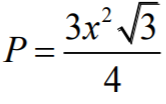
Ponadto z równości
x + h = 24
otrzymujemy
h = 24 – x
gdzie
0 < x < 24
Zatem objętość tego ostrosłupa jest określona wzorem:
czyli
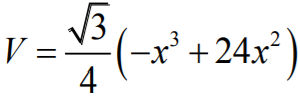
Należy obliczyć, dla jakiego x spełniającego nierówność 0 < x < 24 funkcja V określona
wzorem
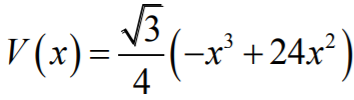
przyjmuje wartość największą.
Rozważamy funkcję
określoną dla każdej liczby rzeczywistej x.
Wyznaczamy pochodną tej funkcji ƒ:
Następnie obliczamy miejsca zerowe pochodnej:
Ponadto:
- ƒ'(x) < 0 w każdym z przedziałów (–∞, 0) oraz (16, +∞)
- ƒ'(x) > 0 w przedziale (0, 16)
Ponieważ
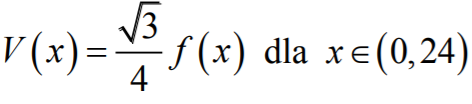
więc w przedziale
x∈(0,24) funkcja
V(x) ma
ekstremum w tym samym punkcie, w którym funkcja
ƒ(x).
Stąd wynika, że w punkcie
x = 16
funkcja V przyjmuje wartość największą.
Objętość ostrosłupa jest równa:
Objętość ostrosłupa prawidłowego trójkątnego jest największa i równa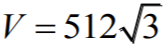 , gdy
promień okręgu opisanego na podstawie jest równy
16.
, gdy
promień okręgu opisanego na podstawie jest równy
16.