Odpowiedź:
Niech punkty C i D leżą na paraboli
y = 2x2 + 2, a punkty E i F leżą na odcinku AB (zob.
rysunek). Oznaczmy przez
x
odległość punktu D od osi Oy.
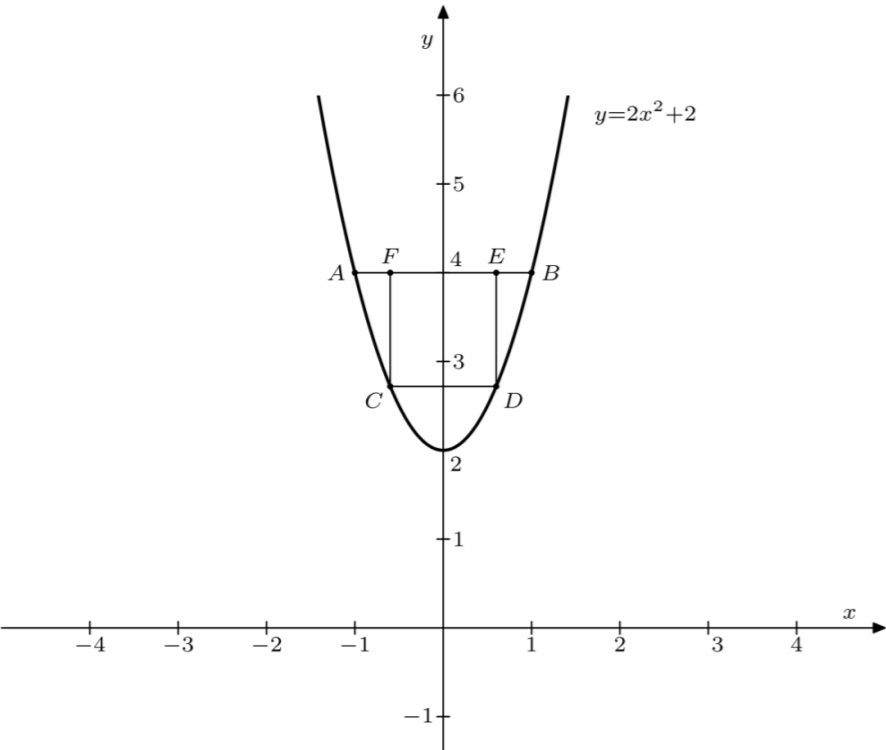
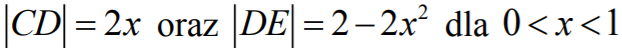
Zatem pole prostokąta CDEF jest określone wzorem: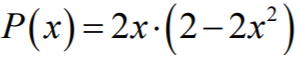
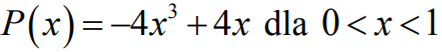
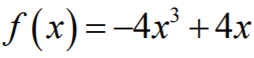
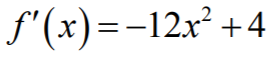
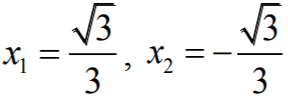
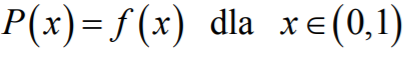
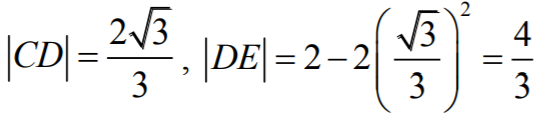

Wówczas punkt D ma współrzędne
D = (x, 2x2 + 2)
punkt C ma współrzędne
C = (–x, 2x2 + 2)
Punkty E i F leżą na prostej o równaniu
y = 4
, zatem ich współrzędne
są równe:
E = (x, 4) i
F = (–x, 4)
Wyznaczamy długości boków CD i DE prostokąta CDEF:
czyli
Rozważamy funkcję
określoną dla każdej liczby rzeczywistej x.
Wyznaczamy pochodną tej funkcji ƒ:
Następnie obliczamy miejsca zerowe pochodnej:
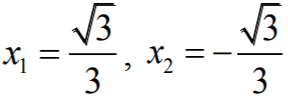
Ponadto:
- ƒ'(x) < 0 w każdym z przedziałów
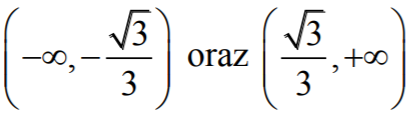
- ƒ'(x) > 0 w przedziale
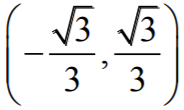
Zatem funkcja ƒ jest malejąca w każdym z przedziałów 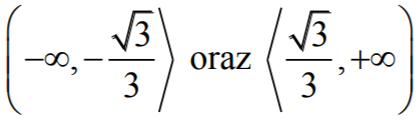 i rosnąca w przedziale
i rosnąca w przedziale 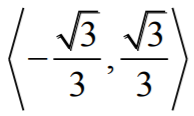 .
.
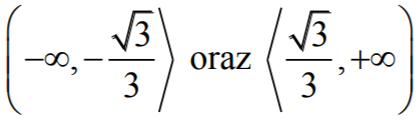 i rosnąca w przedziale
i rosnąca w przedziale 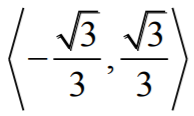 .
.Ponieważ
więc w przedziale
x∈(0,1) funkcja
P(x) ma
ekstremum w tym samym punkcie, w którym funkcja
ƒ(x).
Stąd wynika, że w punkcie 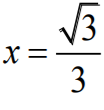 funkcja P przyjmuje wartość największą.
funkcja P przyjmuje wartość największą.
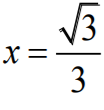 funkcja P przyjmuje wartość największą.
funkcja P przyjmuje wartość największą.Obliczamy wymiary prostokąta:
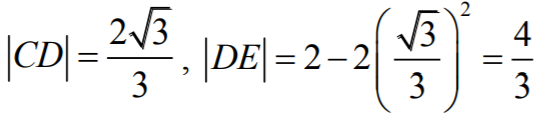
Największe pole ma prostokąt o wymiarach 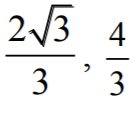 . Jest ono równe
. Jest ono równe 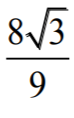 .
.
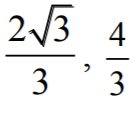 . Jest ono równe
. Jest ono równe