Odpowiedź:
Niech 2x + 5 oznacza długość dłuższej podstawy, a h wysokość trapezu.
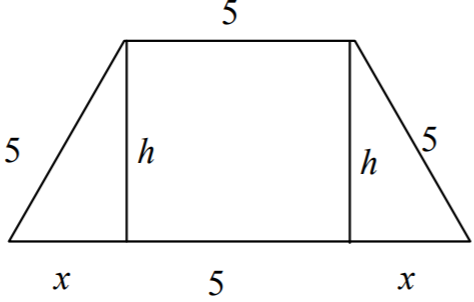
Pole tego trapezu
jest określone wzorem
Z twierdzenia Pitagorasa otrzymujemy zależność
Pole tego trapezu jest określone wzorem
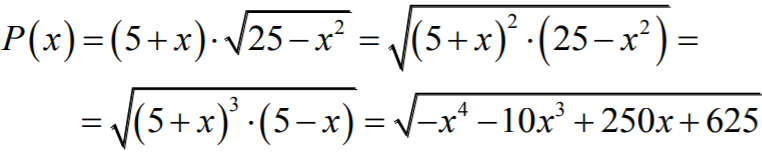
gdzie 0 < x < 5.
przyjmuje wartość największą.
Ponieważ funkcja pierwiastkowa 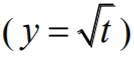 jest rosnąca, więc wystarczy zbadać funkcję
jest rosnąca, więc wystarczy zbadać funkcję 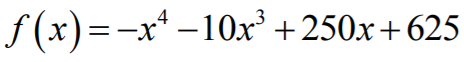 .
.
Wyznaczamy pochodną tej funkcji:
Następnie obliczamy miejsca zerowe pochodnej:
Ponadto:
- ƒ'(x) < 0 w przedziale
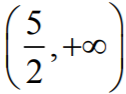
- ƒ'(x) > 0 w każdym z przedziałów
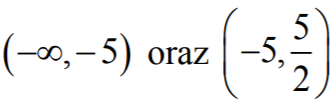
- ƒ'(–5) = 0
Zatem funkcja ƒ jest malejąca w przedziale 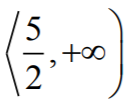 i rosnąca w przedziale
i rosnąca w przedziale 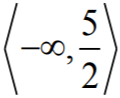 .
.
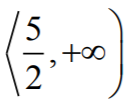 i rosnąca w przedziale
i rosnąca w przedziale Ponieważ
więc w przedziale (0,5) funkcja
P
ma ekstremum
w tym samym punkcie, w którym funkcja
ƒ.
Stąd wynika, że w punkcie 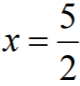 funkcja P
przyjmuje wartość największą.
funkcja P
przyjmuje wartość największą.
Zauważmy wreszcie, że jeżeli 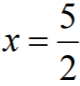 , to 2x + 5= 10. Zatem dłuższa podstawa ma długość 10.
Obliczamy największe pole trapezu dla
, to 2x + 5= 10. Zatem dłuższa podstawa ma długość 10.
Obliczamy największe pole trapezu dla 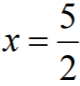 :
:
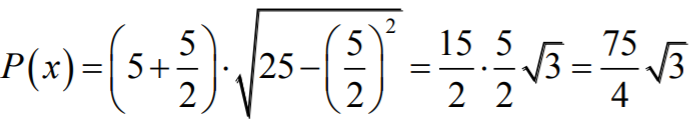
Największe pole ma trapez, którego dłuższa podstawa ma długość 10. Pole tego trapezu jest
równe 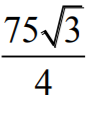 .
.