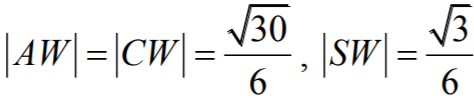Odpowiedź:
Łączymy punkty
A
i
S , A
i
C
oraz
C
i
S
(zobacz rysunek). Niech
T
oznacza punkt przecięcia przekątnych
AC
i
BD
podstawy tego sześcianu.
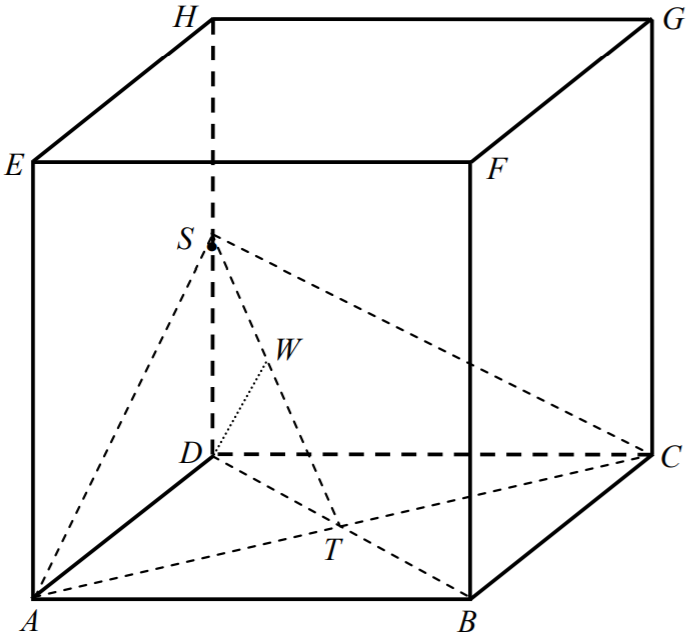
Punkt
S
leży na krawędzi
DH, więc
AS = CS, a zatem trójkąt
ACS, stanowiący podstawę
ostrosłupa
ACSD, jest trójkątem równoramiennym. Wynika stąd, że odcinek
ST
jest
wysokością tego trójkąta.
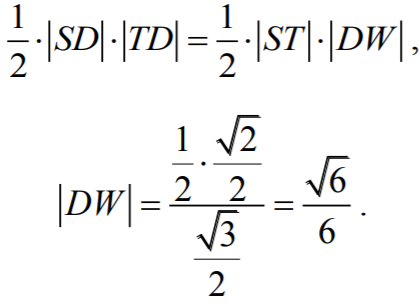
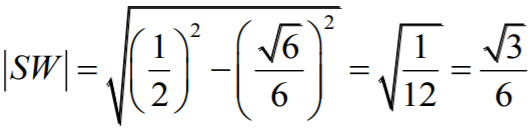
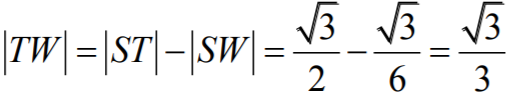
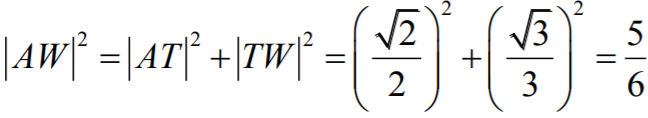
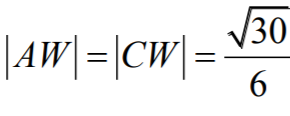
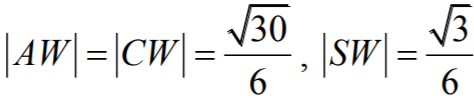

Długość odcinka
ST
obliczamy stosując twierdzenie Pitagorasa do
trójkąta prostokątnego
TSD: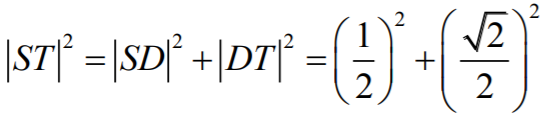
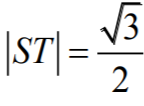
Zauważamy, że odcinek
DW
jest wysokością trójkąta prostokątnego
TDS
poprowadzoną do
przeciwprostokątnej
TS.
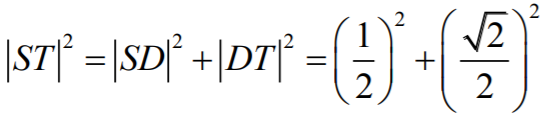
czyli
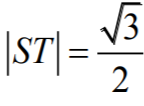
Długość odcinka
DW
obliczymy zapisując na dwa sposoby pole
trójkąta
TDS:
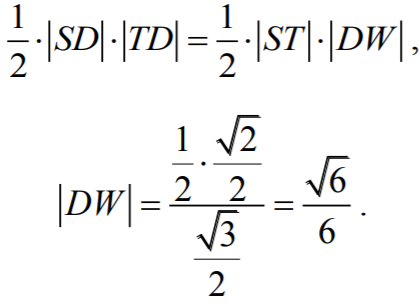
Stąd i z twierdzenia Pitagorasa zastosowanego do trójkąta prostokątnego
SWD
wynika, że:
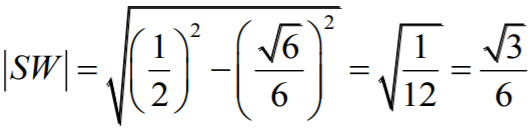
Teraz zauważamy, że wysokość
ST
trójkąta równoramiennego
ACS
jest zawarta w osi
symetrii tego trójkąta. Wynika stąd, że
AW = CW.
Długość odcinka
AW
obliczamy stosując
twierdzenie Pitagorasa do trójkąta prostokątnego
ATW, w którym
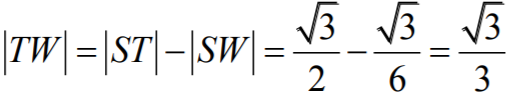
Otrzymujemy zatem
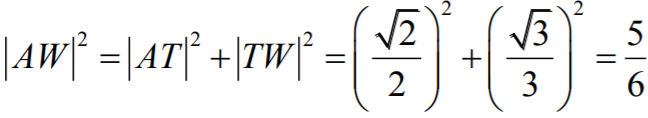
skąd
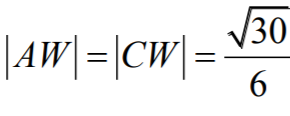
Podsumowując, szukane odcinki mają długości: