Odpowiedź:
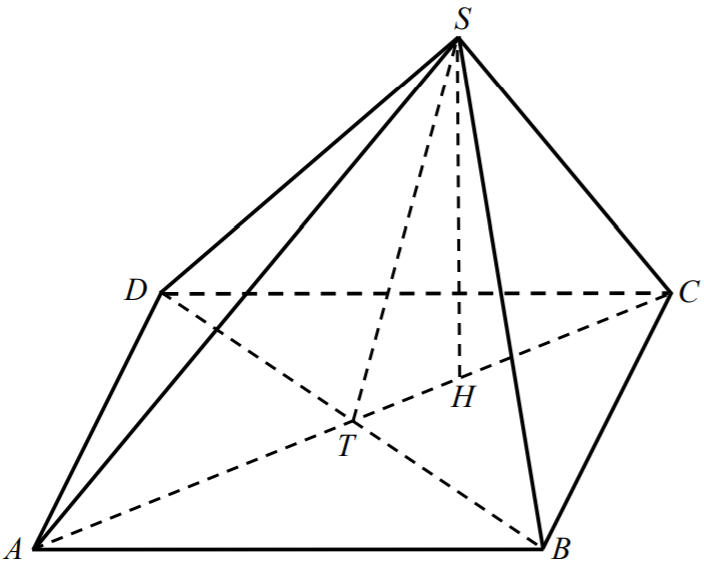
Niech
T
oznacza punkt przecięcia przekątnych
AC
i
BD
podstawy ostrosłupa
(zobacz rysunek).
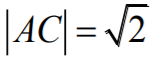
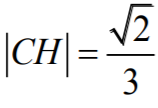
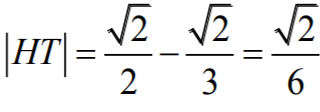
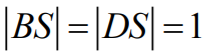
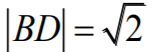
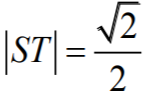
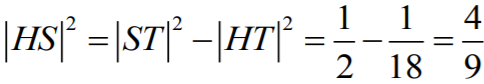
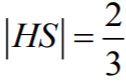
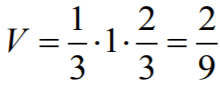
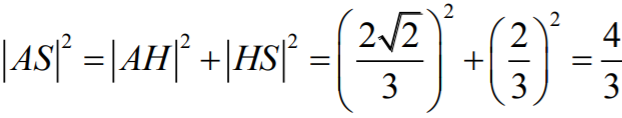
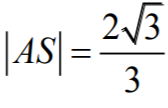
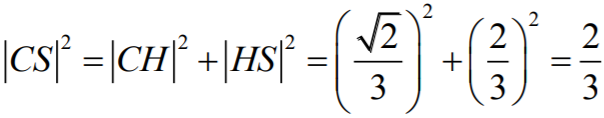
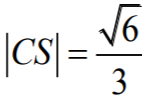

Ponieważ
więc
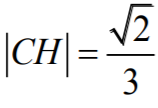
oraz
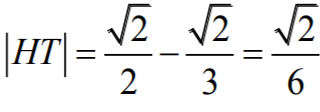
Trójkąt
BSD
jest
równoramiennym trójkątem prostokątnym, dlatego że jego ramiona mają długości
a podstawa
Stąd wynika, że
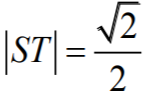
Obliczamy zatem
wysokość
HS
tego ostrosłupa, stosując twierdzenie Pitagorasa do trójkąta
SHT:
skąd wynika, że
Objętość
V
tego ostrosłupa jest zatem równa:
Pozostaje obliczyć jeszcze długości krawędzi bocznych
AS
i
CS.
Z twierdzenia Pitagorasa
zastosowanego dwukrotnie, najpierw do trójkąta
AHS, otrzymujemy
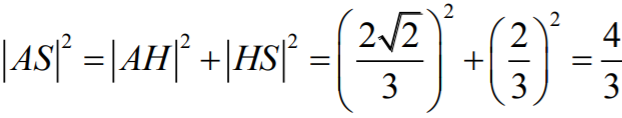
więc
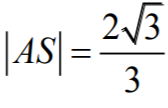
natomiast do trójkąta
CHS
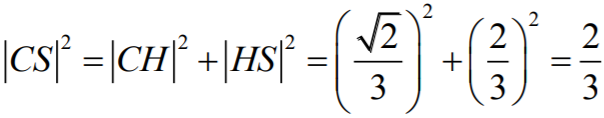
skąd
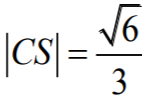
Uwaga
Rozważany ostrosłup nie jest prawidłowy, a wszystkie ściany boczne tego ostrosłupa są
trójkątami równoramiennymi.