Rozważamy kwadrat EFGH . Niech T oznacza punkt przecięcia przedłużeń odcinków QR i EF (zobacz rysunek).

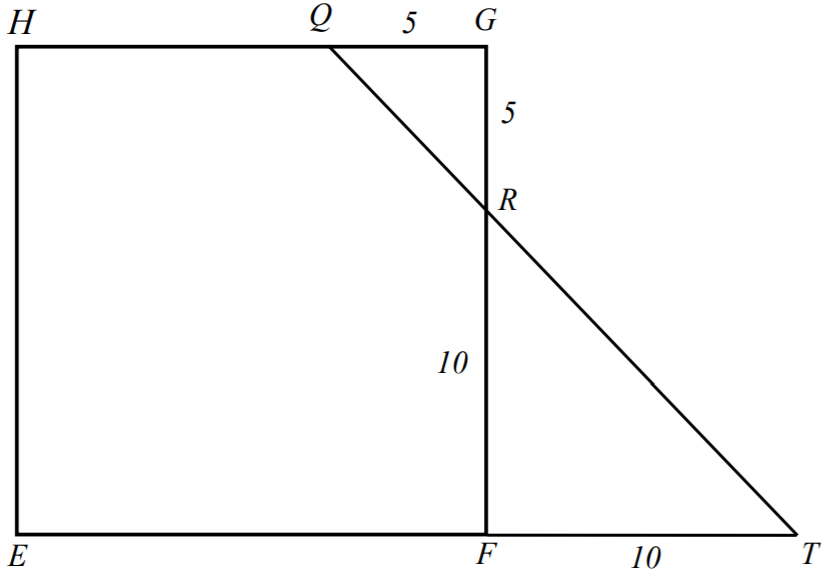
Trójkąty prostokątne RFT i RGQ są podobne na mocy cechy kkk. Stąd wynika, że

|FT| =10

Teraz rozważamy kwadrat ABFE (zobacz rysunek).

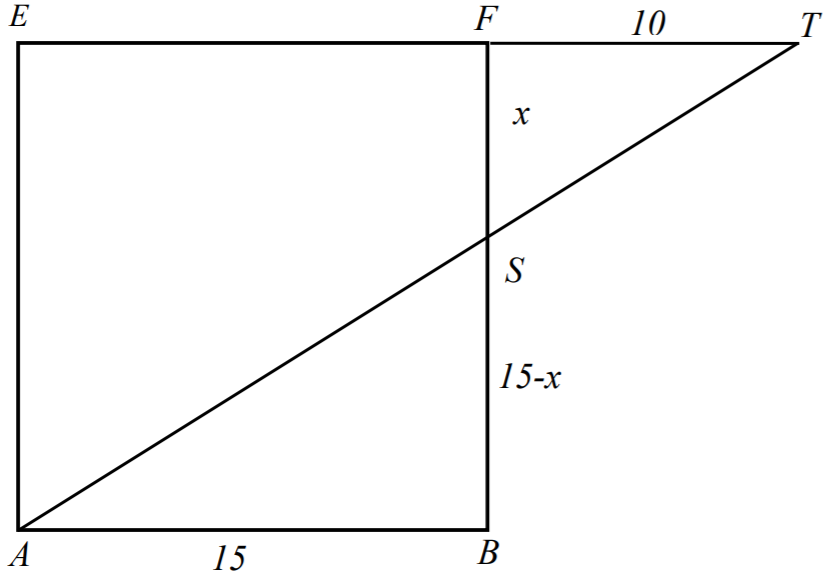
Trójkąty prostokątne ABS i TFS są podobne na mocy cechy kkk. Możemy więc zapisać równanie

Rozwiązujemy to równanie

Zatem długość szukanego odcinka BS jest równa 9.

Ponieważ punkty B i D leżą symetrycznie względem płaszczyzny ACGE, więc

|DP| = |BS| = 9

Rysujemy przekątne AC, BD, EG oraz łączymy punkty P i S. Oznaczmy kolejno:

W - środek odcinka PS,

W₁ - punkt przecięcia przekątnych AC i BD,

T - środek odcinka QR (zobacz rysunek).

Niech ponadto T₁ będzie takim punktem przekątnej AC, że GT = CT₁.

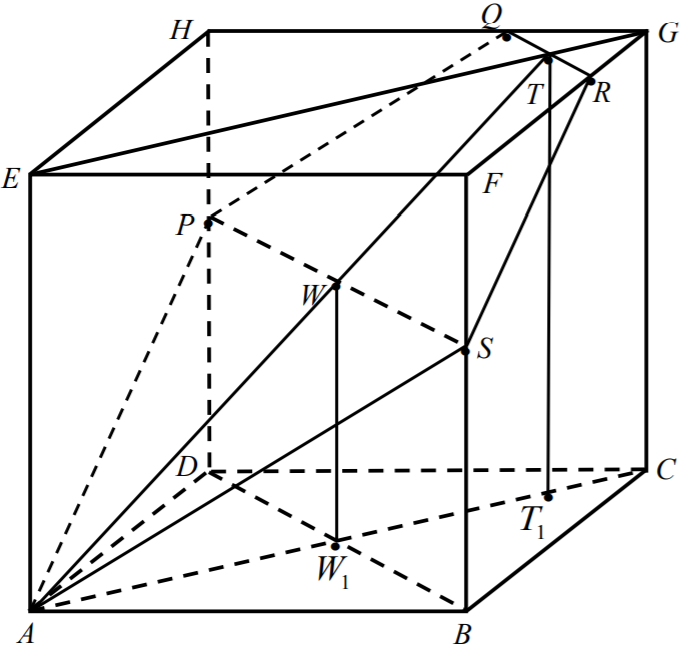
Zauważamy, że DP = BS co wynika, z symetrii względem płaszczyzny ACGE.

Zatem czworokąt BSPD jest prostokątem.

Stąd wynika, że prosta przechodząca przez środki boków tego prostokąta - punkty W i W₁ - jest prostopadła do płaszczyzny ABCD.

Ponadto, prosta przechodząca przez punkty T i T₁ jest także prostopadła do tej płaszczyzny.

Zauważamy, że punkty: A, W, W₁, T i T₁ leżą w jednej płaszczyźnie - jest nią płaszczyzna ACGE.

Na mocy cechy kkk, trójkąty prostokątne AWW₁ i ATT₁ są podobne, więc możemy zapisać równość

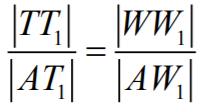
skąd wynika, że

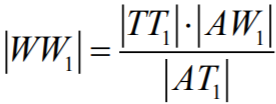
Ponieważ

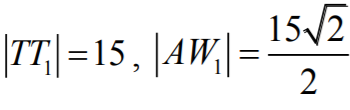
oraz

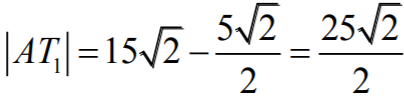
więc

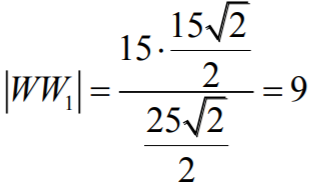
Oczywiście