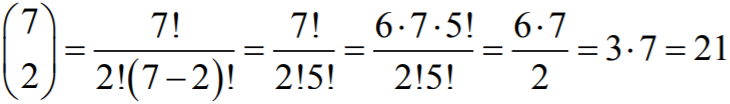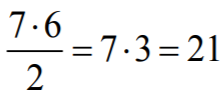Odpowiedź:
Rozwiązanie zadania składa się z trzech kroków. W kroku pierwszym obliczamy, na ile
sposobów można wybrać dwa miejsca (spośród siedmiu), na których stoją cyfry parzyste. Ten
krok możemy wykonać czterema sposobami.

- Możemy skorzystać ze wzoru na liczbę dwuelementowych kombinacji ze zbioru
siedmioelementowego; wyraża się ona współczynnikiem dwumianowym
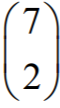 . Ten
współczynnik możemy odczytać z trójkąta Pascala lub obliczyć ze wzoru
. Ten
współczynnik możemy odczytać z trójkąta Pascala lub obliczyć ze wzoru
Mamy zatem
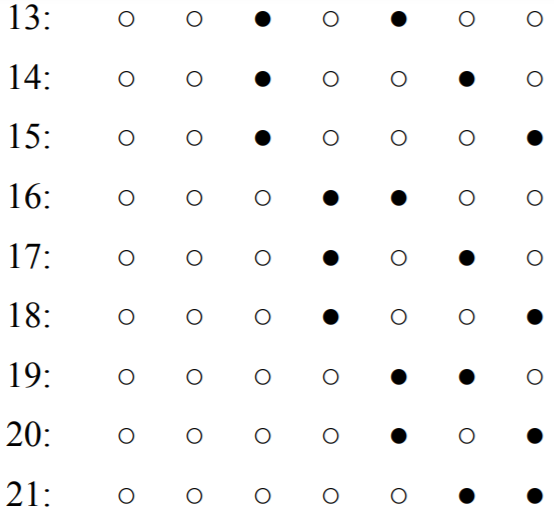
- Możemy po prostu wszystkie te sposoby wyboru dwóch miejsc wypisać (kółko białe oznacza miejsce dla cyfry nieparzystej, kółko czarne — dla parzystej):
- Możemy także te możliwości zliczać: jeśli pierwsza (licząc od lewej strony) cyfra parzysta stoi na pierwszym miejscu, to drugą możemy ustawić na jednym z sześciu miejsc (od drugiego do siódmego); jeśli pierwsza (od lewej strony) cyfra parzysta stoi na drugim miejscu, to drugą możemy ustawić na jednym z pięciu miejsc i tak dalej. Wreszcie, jeśli pierwsza cyfra parzysta stoi na szóstym miejscu, to druga może stać tylko na miejscu siódmym. Łącznie mamy więc
6 + 5 + 4 + 3 + 2 + 1 = 21 sposobów wyboru dwóch miejsc dla cyfr parzystych.
- Możemy wreszcie rozumować następująco: jedną cyfrę parzystą możemy ustawić na jednym z 7 miejsc, drugą na jednym z sześciu miejsc. W ten sposób każde ustawienie policzyliśmy dwukrotnie, np. ustawienie
możemy otrzymać wybierając najpierw miejsce trzecie, a potem miejsce piąte lub wybierając najpierw miejsce piąte, a potem miejsce trzecie. Zatem liczba sposobów wyboru tych dwóch miejsc jest równa
W kroku drugim obliczamy, na ile sposobów możemy na miejscach wybranych dla cyfr
parzystych i nieparzystych napisać te cyfry. Skorzystamy dwukrotnie z reguły mnożenia.
Najpierw na wybranych dwóch miejscach ustawiamy cyfry parzyste. Ponieważ w zapisie
liczby nie występuje zero, więc na każdym miejscu mamy do wyboru cztery cyfry: 2, 4, 6, 8.
Mamy zatem 42 = 16 sposobów zapisania cyfr parzystych na wybranych miejscach. Wreszcie
na każdym z pozostałych pięciu miejsc zapisujemy jedną z pięciu cyfr nieparzystych: 1, 3, 5,
7, 9. Mamy zatem
55 = 3125 sposobów zapisania cyfr nieparzystych na pozostałych
miejscach.
W kroku trzecim obliczamy, ile jest liczb siedmiocyfrowych spełniających warunki opisane
w zadaniu. Korzystamy jeszcze raz z reguły mnożenia i otrzymujemy
liczb.