Odpowiedź:
Zauważmy najpierw, że istnieje tylko 27 liczb trzycyfrowych, których cyfry są wybrane
spośród cyfr 1, 2 i 3. Pierwszą cyfrę możemy bowiem wybrać na 3 sposoby, drugą także na
trzy sposoby (cyfry mogą się powtarzać) i trzecią też na trzy sposoby. Najprostszy sposób
rozwiązania zadania polega zatem na wypisaniu i dodaniu (np. na kalkulatorze) tych liczb.
Oto one:
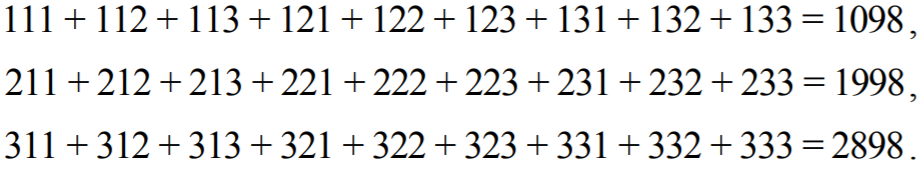
Suma wszystkich liczb jest równa
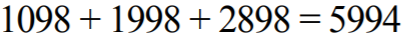
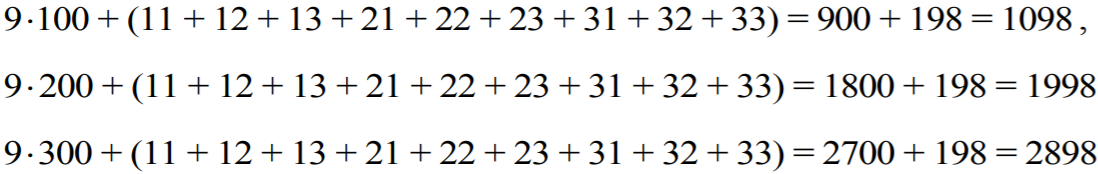
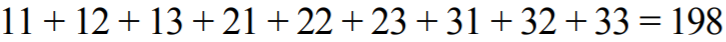
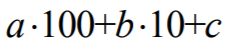
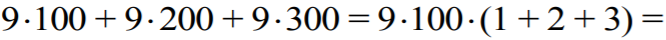
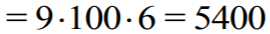
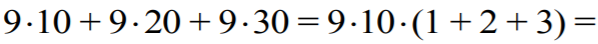
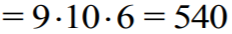
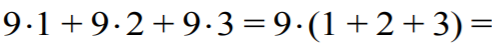
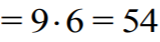
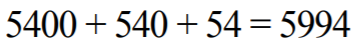
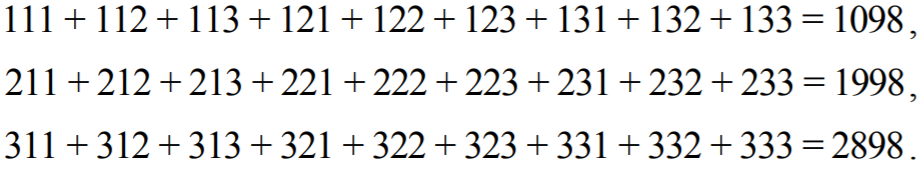
Liczby te można łatwo dodać bez używania kalkulatora. Zauważmy, że sumy liczb w trzech
wierszach są równe:
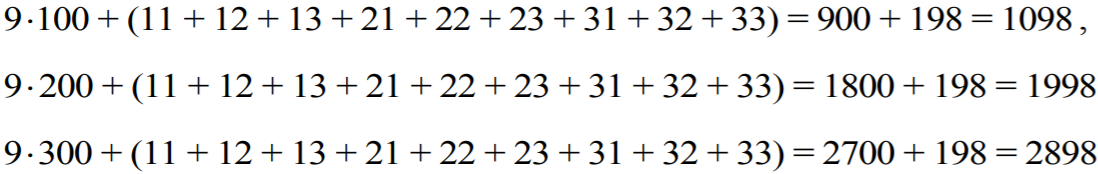
Dodawanie
może być wykonane w pamięci; pozostałe dodawania można łatwo wykonać też w pamięci
lub pisemnie. Najważniejsze było zauważenie, że we wszystkich dodawaniach występowała
ta sama suma liczb dwucyfrowych i zmieniały się tylko sumy setek. Ta obserwacja będzie
podstawą dla drugiego sposobu rozwiązania.
Obliczając sumę wszystkich 27 liczb, każdą z tych liczb zapiszemy w postaci
i będziemy oddzielnie dodawać wielokrotności 100, oddzielnie wielokrotności 10 i wreszcie
oddzielnie cyfry jedności. Policzmy, w ilu liczbach jedynka występuje na pierwszym miejscu
(tzn. jako cyfra setek). Otóż na drugim miejscu możemy postawić jedną z trzech cyfr i na
trzecim też jedną z trzech cyfr. Zatem jedynka jest na pierwszym miejscu w dziewięciu
liczbach. W sumie wszystkich dwudziestu siedmiu liczb dziewięć razy wystąpi składnik 100.
Podobnie 9 razy wystąpi składnik 200 i 9 razy wystąpi składnik 300. Zatem składniki postaci
a⋅100
dadzą sumę
Tak samo pokazujemy, że każda cyfra wystąpi 9 razy na drugim miejscu (tzn. jako cyfra
dziesiątek). Zatem składniki postaci
b⋅10
dadzą sumę
Wreszcie tak samo pokazujemy, że każda cyfra wystąpi 9 razy jako cyfra jedności. Suma cyfr
jedności jest zatem równa
Suma wszystkich liczb wynosi zatem