Odpowiedź:
Wszystkie liczby stucyfrowe o sumie cyfr równej 5, w zapisie których występują tylko cyfry
0, 1, 3, 5 możemy podzielić na 4 grupy w zależności od tego, jaka cyfra stoi na pierwszym
miejscu liczby:
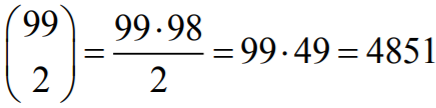
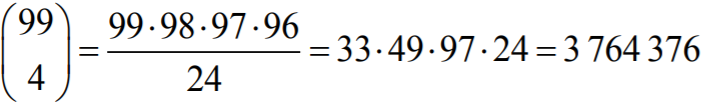
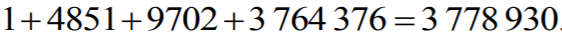
1. Liczba
5000...000 ,w której po cyfrze
5
następuje
99
zer. Jest jedna taka liczba.
2. Liczby postaci
3000...1...000...1...000 , w których po cyfrze
3
występuje
97
cyfr
0
i dwie
cyfry
1, stojące na dwóch miejscach wybranych z
99
możliwych miejsc. Jest
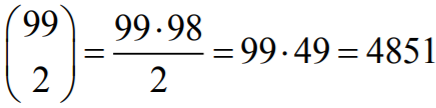
takich liczb.
3. Liczby postaci
1000...3...000...1...000
lub
1000...1...000...3...000 ,
w których po cyfrze
1
występuje
97
cyfr
0
oraz cyfry
1
i
3
(w dowolnej kolejności), stojące na dwóch
miejscach wybranych z
99
możliwych miejsc. Jest
99⋅98 = 9702
takich liczb.
4. Liczby postaci
1000...1...000...1...000...1...000...1...000 , w których po cyfrze
1
występuje
95
cyfr
0
i cztery cyfry
1
, stojące na czterech miejscach wybranych z
99
możliwych
miejsc. Jest
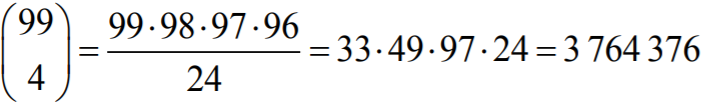
takich liczb.
Zatem wszystkich liczb stucyfrowych o sumie cyfr równej 5, w zapisie których występują
tylko cyfry 0, 1, 3, 5, jest