Odpowiedź:
Przykładowe cztery sposoby rozwiązania tego zadania.
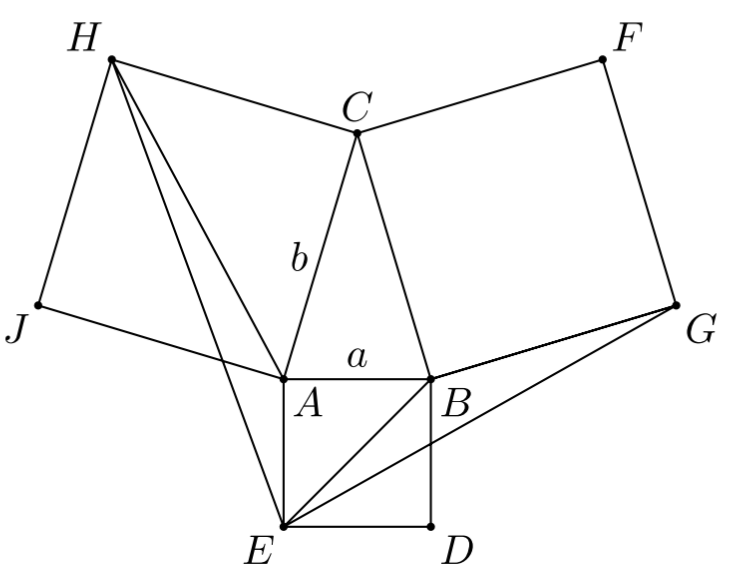
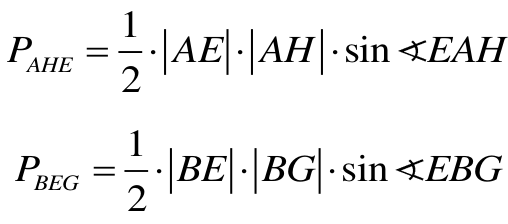
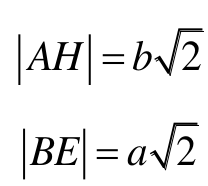
Ponieważ trójkąt ABC jest równoramienny i ostrokątny, więc a > 45°. Następnie
|∢EAB| + |∢BAC| + |∢CAH| = 90° + α + 45° = 135° + α > 135° + 45° = 180°,
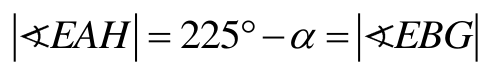
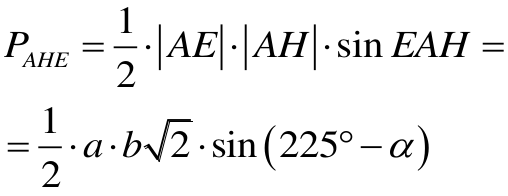
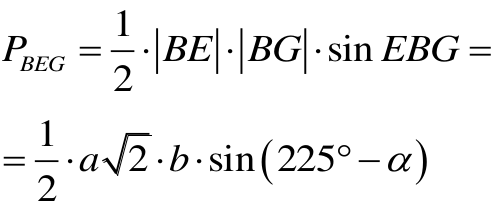
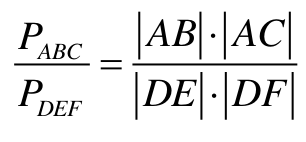
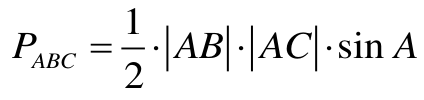

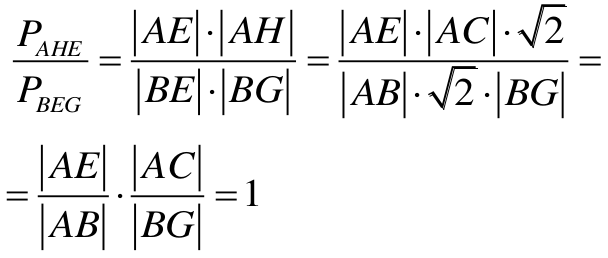
Przy zachowaniu oznaczeń z poprzedniego sposobu rozwiązania, możemy to rozwiązanie
zapisać w sposób następujący.
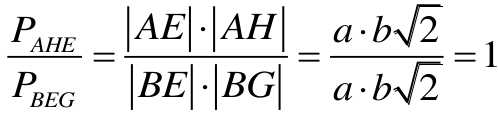
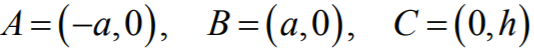
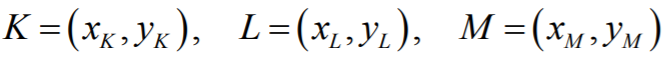
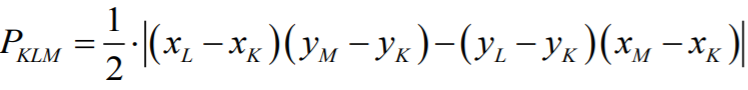
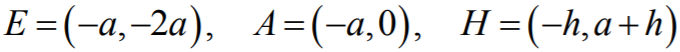

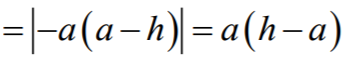
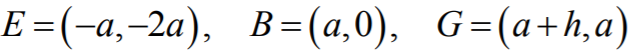
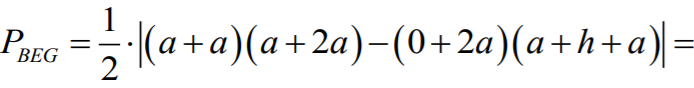
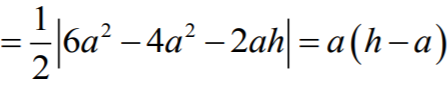
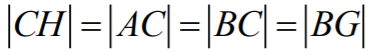
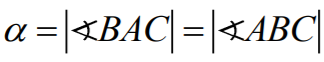
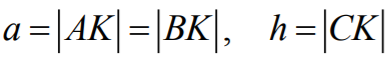
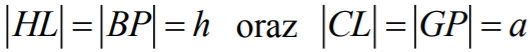
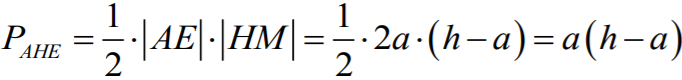
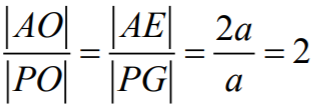

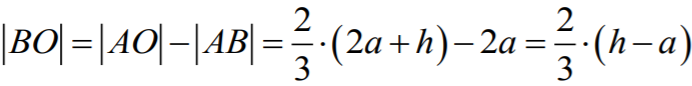

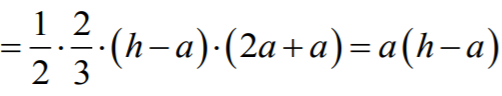
Sposób I (trygonometryczny)
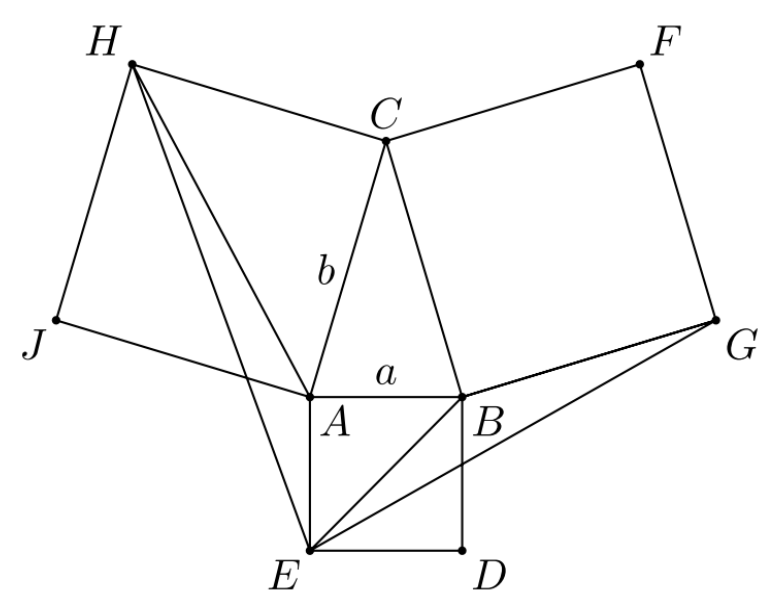
Przyjmijmy oznaczenia:
|AB| = |AE| = a
|AC| = |BC| = |BG| = b
|∢BAC| = |∢ABC| = α
Rozwiązanie tym sposobem polega na obliczeniu obu szukanych pól za pomocą a, b i α.
Mamy bowiem:
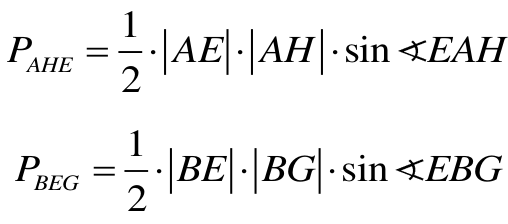
Zauważmy, że: |AE| = a oraz |BG| = b. Obliczamy długości odcinków AH i BE oraz wyrażamy za pomocą a miary kątów EAH i EBG.
Mamy:
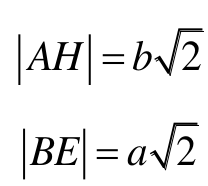
Ponieważ trójkąt ABC jest równoramienny i ostrokątny, więc a > 45°. Następnie
|∢EAB| + |∢BAC| + |∢CAH| = 90° + α + 45° = 135° + α > 135° + 45° = 180°,
a więc kąt wypukły EAH jest równy
360° – (135° + a) = 225° – α
360° – (135° + a) = 225° – α
Podobnie,
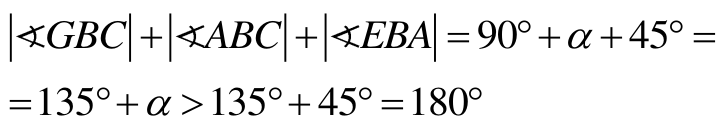
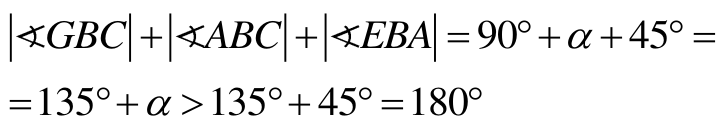
a więc kąt wypukły EBG jest równy
360° – (135° + a) = 225° – α
Zatem
Stąd otrzymujemy
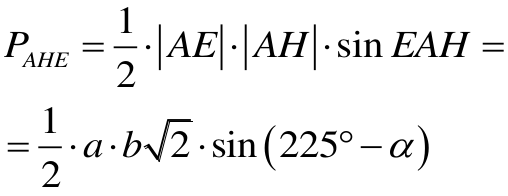
oraz
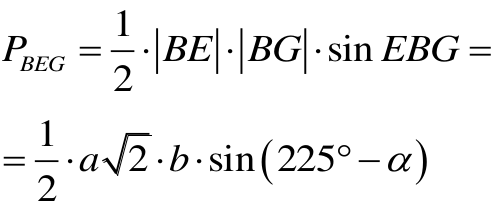
Stąd wynika, że PAHE = PBEG , co kończy dowód.
Komentarz
Rozwiązanie składa się z trzech kroków: obliczenie długości boków AH i BE, wykazanie równości kątów EAH i EBG (np. przez wyznaczenie obu kątów za pomocą α) oraz zastosowanie wzoru na pole trójkąta.
Pokonanie zasadniczych trudności zadania polega na obliczeniu wszystkich wielkości potrzebnych we wzorach na pole. Jeden z możliwych błędów zdających, na który należy zwrócić tu uwagę, może polegać na złym zastosowaniu wzoru na pole trójkąta (np. pominięcie współczynnika ½). Pomimo tego błędu zdający otrzymuje poprawny wynik.
W takim przypadku uznajemy rozwiązanie za niedokończone bezbłędnie zostały pokonane tylko zasadnicze trudności zadania. W tym rozwiązaniu trudno oczekiwać wielu innych rozwiązań błędnych; maturzysta na ogół nie popełni błędu przy obliczaniu przekątnej kwadratu czy dodawaniu miar kątów. Można natomiast spodziewać się rozwiązań częściowych, np. niedokończonych. Niektóre takie rozwiązania omawiamy w uwagach zamieszczonych po schemacie oceniania.
Schemat oceniania I sposobu rozwiązania
Istotny postęp 1p.
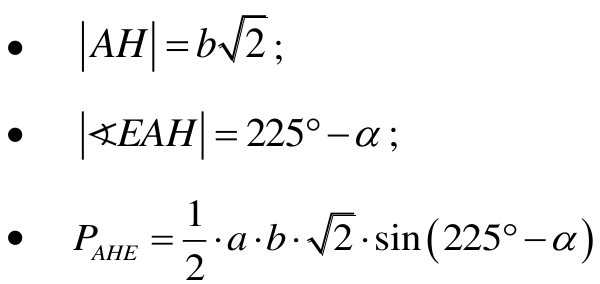
Obliczenie długości boków AH i BE za pomocą boków AB i AC
lub
wykazanie, że |∢EAH| = |∢EBG|
Pokonanie zasadniczych trudności 2p.
Obliczenie długości boków AH i BE za pomocą boków AB i AC oraz wykazanie, że
|∢EAH| = |∢EBG|
Rozwiązanie pełne 3p.
Wykazanie, że pola obu trójkątów są równe.
Uwagi
Zdający może wykonać obliczenia związane tylko z jednym z dwóch trójkątów i na tym skończyć. Na przykład, w przypadku trójkąta AHE może wykonać następujące obliczenia (przyjmując oznaczenia |AB| = a, |AC| = b, |∢BAC| = α )
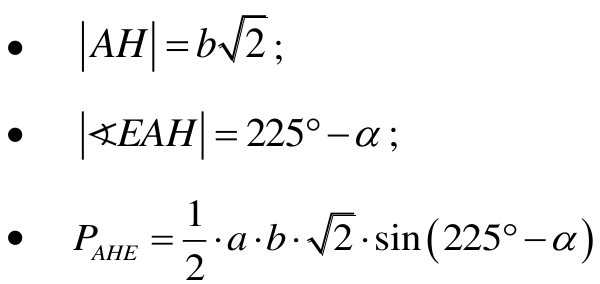
Wówczas:
• jeśli zdający wyznaczy tylko długość boku AH lub miarę kąta EAH, to takie rozwiązanie nie jest jeszcze traktowane jako istotny postęp i przyznajemy za nie 0 punktów,
• jeśli zdający wyznaczy długość boku AH i miarę kąta EAH, to takie rozwiązanie częściowe traktujemy jako „istotny postęp” i przyznajemy za nie 1 punkt,
• jeśli zdający wyznaczy bok AH i zapisze pole w postaci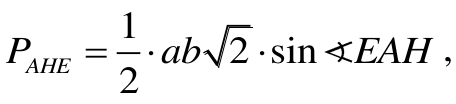 nie
nie
wyznaczając przy tym kąta EAH za pomocą kąta α, to takie rozwiązanie częściowe traktujemy także jako „istotny postęp” i przyznajemy za nie 1 punkt,
• jeśli zdający wyznaczy bok AH, wyznaczy kąt EAH za pomocą kąta α i zapisze pole
trójkąta AHE w postaci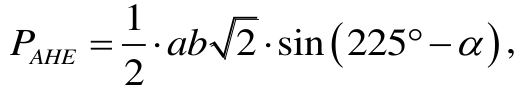 to traktujemy takie rozwiązanie jako pokonanie zasadniczych trudności zadania i przyznajemy za nie 2 punkty.
to traktujemy takie rozwiązanie jako pokonanie zasadniczych trudności zadania i przyznajemy za nie 2 punkty.
• jeśli zdający wyznaczy długość boku AH i miarę kąta EAH, to takie rozwiązanie częściowe traktujemy jako „istotny postęp” i przyznajemy za nie 1 punkt,
• jeśli zdający wyznaczy bok AH i zapisze pole w postaci
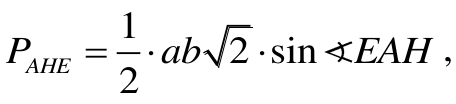 nie
niewyznaczając przy tym kąta EAH za pomocą kąta α, to takie rozwiązanie częściowe traktujemy także jako „istotny postęp” i przyznajemy za nie 1 punkt,
• jeśli zdający wyznaczy bok AH, wyznaczy kąt EAH za pomocą kąta α i zapisze pole
trójkąta AHE w postaci
Sposób II (stosunek pól)
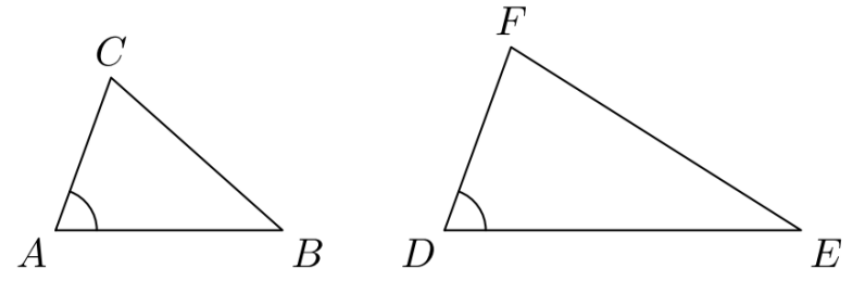
W tym rozwiązaniu korzystamy z następującej własności trójkątów:
Dane są dwa trójkąty ABC i DEF takie, że
∢A = ∢D

Wówczas
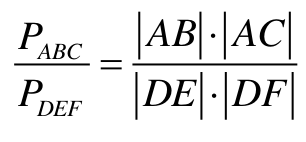
Powyższa proporcja wyraża w sposób czysto geometryczny tę samą treść co wzór trygonometryczny na pole trójkąta. Mianowicie mamy:
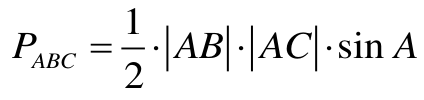
oraz

Sformułowanie geometryczne pozwala przeprowadzić dowód bez odwoływania się do trygonometrii.
Tak jak w sposobie pierwszym dowodzimy, że
|∢EAH| = |∢EBG|

Następnie korzystamy ze wspomnianej wyższej własności trójkątów:
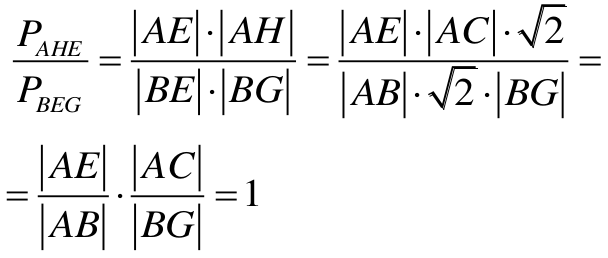
co dowodzi, że PAHE = PBEG
Przyjmujemy |AB| = a i |AC| = b
Wówczas
|AH| = b√2 oraz
EB = a√2
Tak jak w sposobie I, pokazujemy, że
|∢EAH| = |∢EBG|.
Korzystając
z twierdzenia o stosunku pól, otrzymujemy
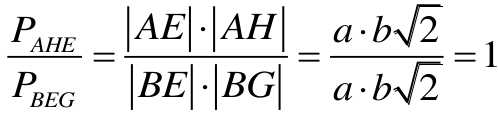
co dowodzi, że PAHE = PBEG
Komentarz
W tym sposobie rozwiązania podstawowym zadaniem jest – tak jak w sposobie pierwszym – obliczenie długości odcinków AH i BE oraz wykazanie równości kątów EAH i EBG.
Dlatego schemat oceniania może być taki sam, jak w sposobie I. Uwagi dotyczące rozwiązań
niekompletnych są takie same jak w przypadku sposobu I.
Schemat oceniania II sposobu rozwiązania
Istotny postęp 1p.
Obliczenie długości boków AH i BE za pomocą boków AB i AC
lub
wykazanie, że |∢EAH| = |∢EBG|
Pokonanie zasadniczych trudności 2p.
Obliczenie długości boków AH i BE za pomocą boków AB i AC oraz wykazanie, że
|∢EAH| = |∢EBG|
Rozwiązanie pełne 3p.
Wykorzystanie wzoru trygonometrycznego do obliczenia pól obu trójkątów i wykazania, że te pola są równe.
Uwaga
Jeśli zdający wykonuje obliczenia tylko w jednym z rozważanych trójkątów, to w istocie
rozwiązuje zadanie sposobem pierwszym i możemy zastosować rozstrzygnięcia zawarte
w uwadze do schematu oceniania w sposobie I.
Sposób III (geometria analityczna)
Rozwiązanie zadania sposobem analitycznym składa się z trzech kroków.
Po pierwsze,
w wygodny sposób umieszczamy rozważane figury geometryczne w układzie współrzędnych - lub równoważnie - do istniejących figur dobieramy układ współrzędnych.
Po drugie,
w przyjętym układzie współrzędnych obliczamy współrzędne potrzebnych punktów.
Wreszcie, za pomocą obliczonych współrzędnych, obliczamy wielkości, o które chodzi
w zadaniu.
W naszym przypadku te kroki sprowadzają się do:
- wyboru układu współrzędnych;
- obliczenia współrzędnych wierzchołków trójkątów AHE i BEG;
- obliczenia pól trójkątów AHE i BEG.
Popatrzmy teraz, w jaki sposób można przeprowadzić takie rozwiązanie. Najpierw musimy
wybrać układ współrzędnych. Można to zrobić na wiele sposobów; trudności obliczeniowe
zadania będą zależały od sposobu wyboru układu. Jednym z najwygodniejszych sposobów
jest wybór układu współrzędnych uwzględniający naturalne symetrie figur występujących
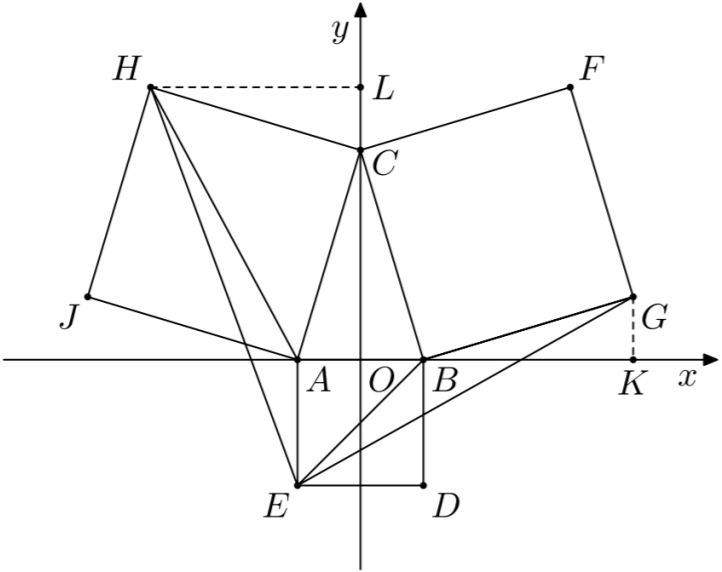
w zadaniu. W naszym przypadku wybieramy układ tak, by oś Oy zawierała oś symetrii
trójkąta równoramiennego ABC. Umieszczamy zatem trójkąt ABC w układzie współrzędnych
tak, że
gdzie
a > 0
i
h > 0. Ponieważ trójkąt ABC jest ostrokątny, więc |∢BAC| > 45°, skąd wynika,
że
a < h.

Wyznaczamy teraz współrzędne punktów E, G i H. Oczywiście bok AB ma długość 2a, skąd
wynika, że
E = (–a, –2a).
Współrzędne punktów G i H możemy wyznaczyć wieloma
sposobami. Pokażemy dokładnie dwa z nich i zasygnalizujemy trzeci sposób, znacznie
bardziej pracochłonny.
- Korzystamy z tego, że jeśli obrócimy wektor [x, y] o 90° zgodnie z ruchem wskazówek zegara, to otrzymamy wektor [y, – x]. (Tę własność można łatwo odczytać z rysunku.) W naszym zadaniu mamy
skądStąd dostajemyW podobny sposób:
- Niech K będzie rzutem punktu G na oś Ox i niech L będzie rzutem punktu H na oś Oy. Wówczas trójkąty CLH i GKB są przystające do trójkąta AOC, skąd
To daje współrzędne punktów.
- Wyznaczamy równanie prostej AC:
oraz równanie prostej prostopadłej do niej, przechodzącej przez punkt C:Następnie na tej prostej prostopadłej znajdujemy oba punkty odległe od punktu C o długość odcinka AC; jest to najbardziej pracochłonna część zadania. Wreszcie wybieramy ten z otrzymanych dwóch punktów, który ma ujemną współrzędną x. W podobny sposób możemy wyznaczyć współrzędne punktu G.
Następnie obliczamy pola trójkątów AHE i BEG. Możemy skorzystać ze wzoru znajdującego
się w zestawie Wybranych wzorów matematycznych. Jeśli wierzchołki trójkąta KLM mają
współrzędne
to pole wyraża się wzorem
W naszym przypadku mamy
skąd dostajemy
Podobnie
skąd dostajemy
To kończy dowód.
Zauważmy też, że pole trójkąta AHE można obliczyć prościej: podstawa AE ma długość 2a,
wysokość (niezaznaczona na rysunku) ma długość
h – a.
Uwaga
Pola trójkątów można też obliczyć inaczej. Można np. wyznaczyć długość jednego boku,
równanie prostej zawierającej ten bok oraz odległość trzeciego wierzchołka od tej prostej
(odpowiednie wzory także znajdują się w tablicach).
Schemat oceniania III sposobu rozwiązania
Istotny postęp 1 pkt
Umieszczenie trójkąta ABC w układzie współrzędnych i podanie współrzędnych jego
wierzchołków.
Pokonanie zasadniczych trudności 2 pkt
Obliczenie współrzędnych punktów E, G i H.
Rozwiązanie pełne 3 pkt
Obliczenie pól trójkątów AHE i BEG np. za pomocą wzorów znajdujących się w tablicach
i zauważenie, że te pola są równe.
Uwaga
Zdający rozwiązujący zadanie tym sposobem mogą popełnić bardzo wiele różnych błędów:
na przykład źle wyznaczyć współrzędne punktów E, G i H lub źle obliczyć pola trójkątów.
Mogą wreszcie wybrać takie metody obliczania pól, że nie będzie oczywiste, czy otrzymane
wyniki są równe (może to wymagać odpowiednich przekształceń). Niezależnie od charakteru
i przyczyny błędu, schemat oceniania wyraźnie wskazuje, jaką liczbę punktów należy
przyznać zdającemu. Maksymalną liczbę punktów zdający otrzymuje za bezbłędnie
wykonane kroki. Może się jednak zdarzyć, że zdający popełni nieistotny błąd rachunkowy
przy wyznaczaniu współrzędnych któregoś punktu i w ten sposób uzyska błędne wyniki
w ostatnim kroku. Jeśli jednak metoda obliczania pól trójkątów jest poprawna, zostały
dokonane poprawne podstawienia do wzorów, zgodne z otrzymanymi wynikami obliczeń
oraz obliczenia w tym kroku zostały wykonane poprawnie, to zdający otrzymuje 2 punkty
(jest to sytuacja, w której zdający doprowadza rozwiązanie do końca, popełniając nieistotny
błąd rachunkowy podczas pokonywania zasadniczych trudności).
Sposób IV (bezpośrednie obliczenie pól)
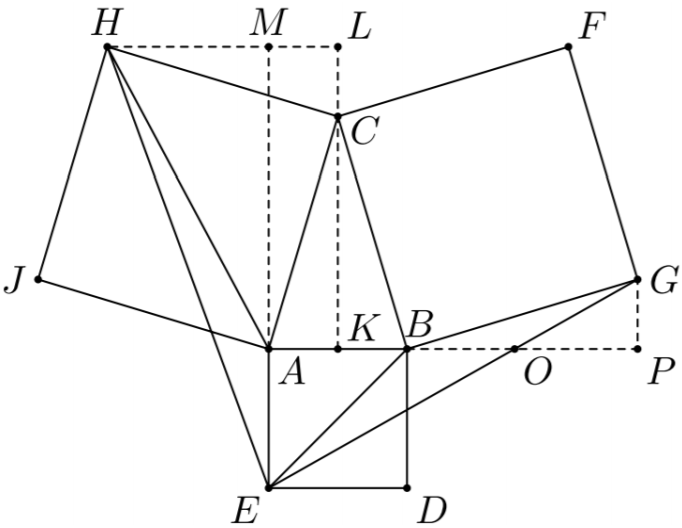
Prowadzimy w trójkącie ABC wysokość CK. Następnie niech punkt L będzie rzutem
prostokątnym punktu H na prostą KC i niech punkt P będzie rzutem prostokątnym punktu G
na prostą AB.

Wówczas nietrudno zauważyć, że trójkąty CLH i BPG są przystające do trójkątów AKC
i BKC. Mianowicie
Jeśli następnie
to 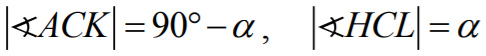 oraz
oraz 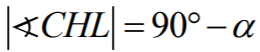 .
.
Podobnie 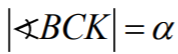 ,
, 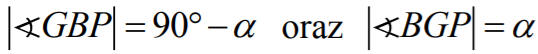 .
.
Wspomniane przystawania trójkątów wynikają teraz
z cechy przystawania kbk.
Przyjmijmy oznaczenia:
Wówczas
Ponadto
a < h.
Niech następnie punkt M
będzie rzutem prostokątnym punktu A na prostą HL. Ponieważ
a < h, więc punkt M leży
wewnątrz odcinka HL. Możemy już obliczyć pole trójkąta EAH. Mianowicie
Następnie niech punkt O będzie punktem przecięcia prostych EG i AP. Z podobieństwa
trójkątów EAO i GPO wynika, że
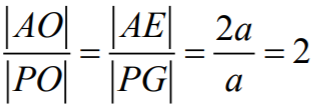
Zatem
skąd wynika, że
Wreszcie
To kończy dowód.
Schemat oceniania IV sposobu rozwiązania
Istotny postęp 1 pkt
Dorysowanie trójkątów CLH i GPB oraz zauważenie, że są one przystające do trójkąta AKC
(lub BKC). Nie wymagamy w tym miejscu od zdającego pełnego dowodu przystawania
– przyjmujemy, że uzasadnienie przystawania jest oczywiste.
Pokonanie zasadniczych trudności 2 pkt
Obliczenie pola jednego z trójkątów AHE i BEG.
Rozwiązanie pełne 3 pkt
Obliczenie pól obu trójkątów i stwierdzenie, że są one równe.
Uwaga
W takim sposobie rozwiązania zadania jest mało prawdopodobne, by zdający popełnił istotny
błąd. Mogą się natomiast zdarzyć rozwiązania niedokończone. Mogą też wystąpić różne inne
próby rozwiązania polegające na dorysowywaniu do rysunku różnych odcinków. Jeśli nie jest
wyraźnie widoczny cel takich poszukiwań i nie został on wyraźnie wskazany w rozwiązaniu,
to zdający otrzymuje 0 punktów.