Odpowiedź:
Omówimy 6 sposobów rozwiązania tego zadania.
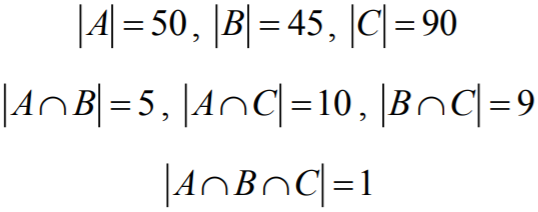
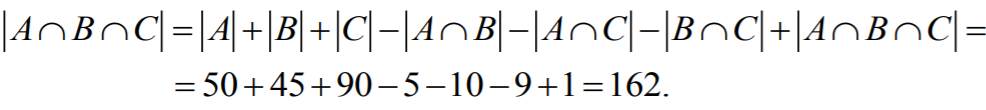
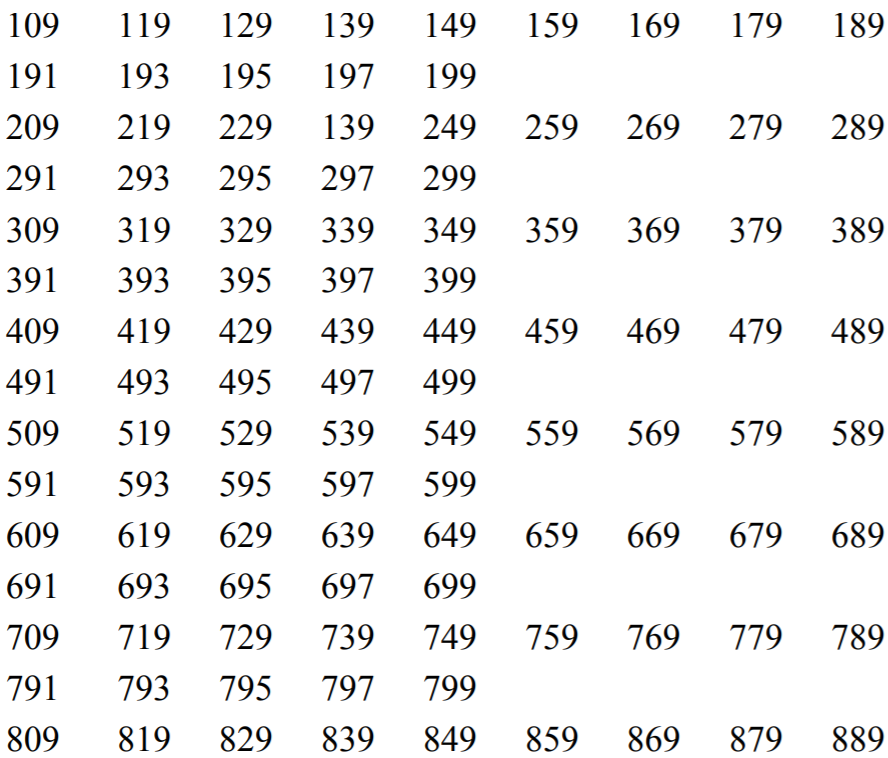

W pierwszych 16 wierszach mamy ośmiokrotnie wiersz z 9 liczbami i wiersz z 5 liczbami.
W następnych 10 wierszach mamy po 5 liczb. Łącznie zatem wypisano
W trakcie wypisywania możemy zauważyć regułę i ją opisać: najpierw występują liczby
zaczynające się od cyfry różnej od 9 (mamy tu 8 możliwości). Dla każdej takiej pierwszej
cyfry c mamy 9 liczb postaci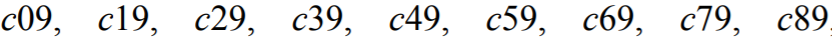
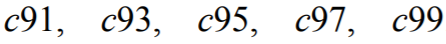
Sposób I (umieszczenie dziewiątki)
W tym sposobie rozwiązania pokażemy najpierw rozumowanie błędne polegające na
policzeniu kilkakrotnym tych samych liczb. Wskazany błąd jest niezwykle często popełniany
przez zdających rozwiązujących to zadanie; można go jednak dość łatwo naprawić.
Wystarczy odjąć liczbę tych liczb, które były policzone dwukrotnie i odjąć podwojoną liczbę
tych liczb, które były policzone trzykrotnie. Obliczenie, ile należy odjąć, jest dość łatwe.
Problem polega jednak na tym, że zdający popełniający ten błąd nie zdają sobie sprawy
z tego, na czym on polega - nie dostrzegają, że niektóre liczby policzyli wielokrotnie.
A oto rozwiązanie. Wiemy, że jedną z cyfr jest 9; możemy ją umieścić na jednym z trzech
miejsc: pierwszym, drugim lub trzecim.
- Jeśli umieścimy dziewiątkę na pierwszym miejscu, to na drugim możemy umieścić dowolną z 10 cyfr, a na trzecim dowolną z pięciu cyfr nieparzystych. Łącznie daje to w tym przypadku 50 liczb.
- Jeśli umieścimy dziewiątkę na drugim miejscu, to na pierwszym możemy umieścić dowolną z 9 cyfr, a na trzecim dowolną z pięciu cyfr nieparzystych. Łącznie daje to w tym przypadku 45 liczb.
- Jeśli umieścimy dziewiątkę na trzecim miejscu, to na pierwszym możemy umieścić dowolną z 9 cyfr, a na drugim dowolną z 10 cyfr. Łącznie daje to w tym przypadku 90 liczb.
50 + 45 + 90 = 185
liczb.
Które liczby zostały policzone wielokrotnie? Popatrzmy na przykład. Przypuśćmy, że
najpierw umieściliśmy cyfrę 9 na pierwszym miejscu, a na pozostałych miejscach
umieściliśmy kolejno cyfry 5 i 9. Otrzymaliśmy liczbę 959. Przypuśćmy teraz, że najpierw
umieściliśmy cyfrę 9 na trzecim miejscu, a następnie umieściliśmy na pierwszych dwóch
miejscach kolejno cyfry 9 i 5. Znów otrzymaliśmy liczbę 959. Ta liczba została więc
w powyższym sposobie zliczania policzona dwukrotnie. Zobaczmy teraz, w jaki sposób
można poprawić to rozwiązanie błędne.
Dostaliśmy wynik 185. Zauważmy jednak, że liczby z dwiema dziewiątkami były policzone
po dwa razy, a liczba 999 nawet trzy razy. Zliczamy teraz liczby z dwiema dziewiątkami.
- Jeśli umieścimy dziewiątkę na pierwszym i drugim miejscu, to na trzecim możemy umieścić dowolną z 4 cyfr nieparzystych: 1, 3, 5 lub 7.
- Jeśli umieścimy dziewiątkę na drugim i trzecim miejscu, to na pierwszym możemy umieścić dowolną z 8 cyfr (od 1 do 8).
- Jeśli umieścimy dziewiątkę na pierwszym i trzecim miejscu, to na drugim możemy umieścić dowolną z 9 cyfr (od 0 do 8).
185 – 21 – 2 = 162
Schemat oceniania I sposobu rozwiązania
Pokazane na początku rozwiązanie błędne zawiera istotne elementy rozumowania
prawidłowego, więc powinno być ocenione jako rozwiązanie częściowe. Uznajemy je za
,,istotny postęp”.
Postęp niewielki 1 pkt
Zdający obliczy, że przy umieszczeniu dziewiątki na pierwszym miejscu otrzyma 50 liczb lub
obliczy, że przy umieszczeniu dziewiątki na drugim miejscu otrzyma 45 liczb, lub obliczy, że
przy umieszczeniu dziewiątki na trzecim miejscu otrzyma 90 liczb.
Istotny postęp 2 pkt
Zdający obliczy, że przy umieszczeniu dziewiątki na pierwszym miejscu otrzyma 50 liczb,
przy umieszczeniu dziewiątki na drugim miejscu otrzyma 45 liczb i przy umieszczeniu
dziewiątki na trzecim miejscu otrzyma 90 liczb. Nie wymagamy, by w tej kategorii otrzymał
wynik łączny 185 liczb.
Pokonanie zasadniczych trudności 4 pkt
Zdający otrzyma wynik 185 liczb, następnie zauważy, że pewne liczby policzono
wielokrotnie oraz obliczy, że 21 liczb policzono dwukrotnie. Za samo zauważenie, że pewne
liczby zostały policzone wielokrotnie, bez podania prawidłowej ich liczby (na przykład
w wyniku błędnego obliczenia), zdający otrzymuje 3 punkty.
Rozwiązanie pełne 5 pkt
Zdający pokona zasadnicze trudności zadania, zauważy, że liczba 999 była policzona
trzykrotnie i obliczy poprawnie liczbę wszystkich rozważanych liczb:
50 + 45 + 90 – 21 – 2 = 162
Sposób II (pierwsza dziewiątka)
Wszystkie interesujące nas liczby dzielimy na trzy grupy i policzymy liczby w każdej grupie.
- Do pierwszej grupy zaliczamy liczby zaczynające się dziewiątką.
- Do drugiej grupy zaliczamy liczby, w których pierwsza dziewiątka znajduje się na drugim miejscu.
- Do trzeciej grupy zaliczamy liczby, w których pierwsza dziewiątka znajduje się na trzecim miejscu.
- W pierwszej grupie znajduje się 50 liczb: na pierwszym miejscu jest dziewiątka, na drugim dowolna z 10 cyfr i na trzecim dowolna z pięciu cyfr nieparzystych.
- W drugiej grupie znajduje się 40 liczb: na pierwszym miejscu znajduje się jedna z 8 cyfr (nie może być 0 i 9), na drugim miejscu jest dziewiątka i na trzecim jedna z pięciu cyfr nieparzystych.
- W trzeciej grupie znajdują się 72 liczby: na pierwszym miejscu znajduje się jedna z 8 cyfr (jak wyżej), na drugim jedna z 9 cyfr (nie może być 9) i na trzecim miejscu znajduje się dziewiątka.
Komentarz
Zdający rozwiązujący zadanie tą metodą zdaje sobie prawdopodobnie sprawę
z niebezpieczeństwa policzenia tych samych liczb wielokrotnie i prawdopodobnie nie popełni
większych błędów. Możliwe są natomiast drobne błędy rachunkowe.
Schemat oceniania II sposobu rozwiązania
Postęp niewielki 1 pkt
Zdający prawidłowo zdefiniuje trzy grupy liczb.
Istotny postęp 2 pkt
Zdający obliczy, ile jest liczb w co najmniej jednej z tych trzech grup.
Pokonanie zasadniczych trudności 4 pkt
Zdający prawidłowo obliczy, ile jest liczb w każdej z tych trzech grup. Za prawidłowy wynik
w dwóch grupach zdający otrzymuje 3 punkty.
Rozwiązanie pełne 5 pkt
Zdający pokona zasadnicze trudności zadania i obliczy poprawnie liczbę wszystkich
rozważanych liczb:
50 + 40 + 72 = 162
Sposób III (liczba dziewiątek)
Najpierw policzymy liczby, w których jest tylko jedna cyfra 9. Tym razem zastosujemy
metodę znaną z powyższego błędnego rozwiązania, jednak użycie tej metody będzie
poprawne, gdyż jest tylko jedna cyfra 9. Możemy umieścić ją na jednym z trzech miejsc.
- Jeśli umieścimy dziewiątkę na pierwszym miejscu, to na drugim możemy umieścić dowolną z 9 cyfr (od 0 do 8), a na trzecim dowolną z czterech cyfr nieparzystych: 1, 3, 5, 7. Łącznie daje to w tym przypadku 36 liczb.
- Jeśli umieścimy dziewiątkę na drugim miejscu, to na pierwszym możemy umieścić dowolną z 8 cyfr (od 1 do 8), a na trzecim dowolną z czterech cyfr nieparzystych: 1, 3, 5, 7. Łącznie daje to w tym przypadku 32 liczby.
- Jeśli umieścimy dziewiątkę na trzecim miejscu, to na pierwszym możemy umieścić dowolną z 8 cyfr (od 1 do 8), a na drugim dowolną z 9 cyfr (od 0 do 8). Łącznie daje to w tym przypadku 72 liczby.
36 + 32 + 72 = 140
liczb.
Teraz policzymy liczby, w których są dwie cyfry 9.
- Jeśli umieścimy dziewiątkę na pierwszym i drugim miejscu, to na trzecim możemy umieścić dowolną z 4 cyfr nieparzystych.
- Jeśli umieścimy dziewiątkę na drugim i trzecim miejscu, to na pierwszym możemy umieścić dowolną z 8 cyfr.
- Jeśli umieścimy dziewiątkę na pierwszym i trzecim miejscu, to na drugim możemy umieścić dowolną z 9 cyfr.
4 + 8 + 9 = 21
liczb.
Wreszcie mamy jedną liczbę z trzema dziewiątkami: 999.
Mamy więc
140 + 21 + 1 = 162
liczby.
Schemat oceniania III sposobu rozwiązania
Istotny postęp 2 pkt
Obliczenie, że istnieje 140 liczb z jedną dziewiątką lub obliczenie, że istnieje 21 liczb
z dwiema dziewiątkami. Każde z tych obliczeń wymaga rozpatrzenia trzech przypadków
w zależności od położenia dziewiątek. Zdający otrzymuje 1 punkt, jeśli prawidłowo
rozpatrzy dwa z tych trzech przypadków i na tym poprzestanie lub popełni błąd w trzecim
obliczeniu lub w obliczeniu sumy.
Pokonanie zasadniczych trudności 4 pkt
Obliczenie, że istnieje 140 liczb z jedną dziewiątką i istnieje 21 liczb z dwiema dziewiątkami.
Jeśli zdający poprawnie wykona jedno z tych obliczeń, a w drugim popełni błąd taki jak
opisany w poprzedniej kategorii, to otrzymuje 3 punkty.
Rozwiązanie pełne 5 pkt
Podanie pełnej odpowiedzi. Jeśli zdający poprawnie obliczy, że istnieje 140 liczb z jedną
dziewiątką lub 21 liczb z dwiema dziewiątkami, drugie z tych obliczeń doprowadzi do końca
z błędem w jednym z trzech przypadków, następnie zauważy, że istnieje dokładnie jedna
liczba z trzema dziewiątkami i poprawnie doda otrzymane liczby – uzyskując w efekcie
wynik błędny – otrzymuje 4 punkty.
Sposób IV (uzupełnianie)
Najpierw policzymy wszystkie liczby trzycyfrowe nieparzyste. Wszystkich liczb
trzycyfrowych jest 900; co druga jest nieparzysta. Istnieje zatem 450 liczb trzycyfrowych
nieparzystych. Możemy również rozumować następująco: na pierwszym miejscu można
umieścić jedną z dziewięciu cyfr, na drugim jedną z dziesięciu cyfr, a na trzecim jedną
z pięciu cyfr nieparzystych: 1, 3, 5, 7, 9. Łącznie mamy zatem 9∙10∙5 = 450 liczb. Teraz
policzymy wszystkie liczby nieparzyste, w których nie występuje cyfra 9. Tym razem na
pierwszym miejscu możemy umieścić jedną z ośmiu cyfr (od 1 do 8), na drugim jedną
z dziewięciu cyfr (od 0 do 8), a na trzecim jedną z czterech cyfr nieparzystych: 1, 3, 5, 7;
łącznie mamy zatem
8∙9∙4 = 288 liczb. Liczby, o które chodzi w zadaniu, to oczywiście
liczby należące do pierwszej grupy (wszystkie liczby nieparzyste) i nienależące do drugiej
grupy (w której są liczby nieparzyste bez dziewiątki). Stąd wynika, że liczb, o które chodzi
w zadaniu, jest
450 – 288 = 162.
Schemat oceniania IV sposobu rozwiązania
Postęp niewielki 1 pkt
Obliczenie liczby liczb trzycyfrowych: 900.
Istotny postęp 2 pkt
Obliczenie liczby nieparzystych liczb trzycyfrowych: 450. Jeśli zdający oblicza tę liczbę
metodą rozmieszczania cyfr i popełni błąd rachunkowy, to otrzymuje 1 punkt. Jeśli zdający
stwierdzi, że istnieje 899 liczb trzycyfrowych i jako liczbę nieparzystych liczb trzycyfrowych
poda liczbę 449 lub 450, to otrzymuje 1 punkt.
Pokonanie zasadniczych trudności 4 pkt
Obliczenie liczby nieparzystych liczb trzycyfrowych niezawierających cyfry 9: jest 288 liczb.
Jeżeli zdający obliczy poprawnie liczbę nieparzystych liczb trzycyfrowych niezawierających
cyfry 9, ale popełni błąd opisany w kategorii ,,istotny postęp'”, to otrzymuje 3 punkty.
Rozwiązanie pełne 5 pkt
Zdający otrzyma prawidłowy wynik (162 liczby), nie popełniając przy tym błędu
(np. opisanego w kategorii ,,istotny postęp”). W przypadku gdy popełni taki błąd, otrzymuje
4 punkty.
Sposób V (zasada włączeń i wyłączeń)
Niektórzy zdający mogą zastosować w rozwiązaniu zasadę włączeń i wyłączeń, choć nie ma
jej w podstawie programowej - mogli ją na przykład odkryć samodzielnie jako regułę niemal
oczywistą intuicyjnie.
Niech A będzie zbiorem liczb nieparzystych z dziewiątką na pierwszym miejscu, B zbiorem
liczb nieparzystych z dziewiątką na drugim miejscu i wreszcie C zbiorem nieparzystych
z dziewiątką na trzecim miejscu. Zbiorem liczb, które nas interesują, jest oczywiście zbiór
A∪B∪C. Nietrudno teraz zauważyć, że:
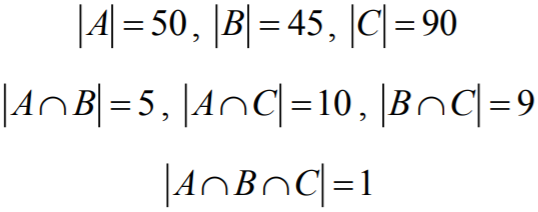
Z zasady włączeń i wyłączeń dostajemy
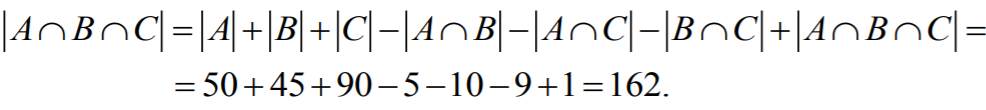
Schemat oceniania V sposobu rozwiązania
Postęp niewielki 1 pkt
Zdający zdefiniuje zbiory A, B i C i zauważy, że ma obliczyć 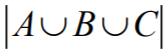 .
.
Postęp większy 2 pkt
Zdający obliczy 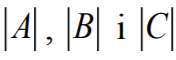 .
.
Istotny postęp 3 pkt
Zdający obliczy 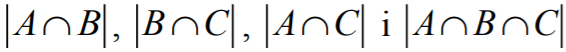 .
.
Pokonanie zasadniczych trudności 4 pkt
Zdający poprawnie zapisze wzór włączeń i wyłączeń i podstawi do niego prawidłowe dane.
Jeśli zdający zdefiniuje zbiory A, B i C, poprawnie zapisze wzór włączeń i wyłączeń
i poprawnie obliczy co najmniej |A|, |B| i |C| oraz popełni błędy w pozostałych obliczeniach,
to otrzymuje 3 punkty.
Rozwiązanie pełne 5 pkt
Uwaga
Jeśli zdający tylko zdefiniuje zbiory A, B i C oraz poprawnie zapisze wzór włączeń
i wyłączeń, to otrzymuje 2 punkty.
Sposób VI (wypisywanie liczb w kolejności rosnącej)
Ten sposób rozwiązania, z pozoru nierozsądny, może jednak naprowadzić zdającego na
stosunkowo proste rozwiązanie. Oczywiście wypisywanie wszystkich liczb spełniających
warunki zadania nie może być dokonywane bez zastanowienia. Nie chodzi zatem o wypisanie
w kolejności rosnącej wszystkich liczb trzycyfrowych (jest ich 900), wykreślenie liczb
parzystych oraz liczb, w których nie występuje dziewiątka i zliczeniu liczb niewykreślonych.
Jeśli zdający nie popełni błędu, powinien otrzymać 162 liczby. Oczywiście takie rozwiązanie,
wykonane bezbłędnie, powinno być ocenione na 5 punktów.
Zdający może również wypisywać w kolejności rosnącej tylko właściwe liczby. Oto
poprawny wynik:


8∙(9 + 5) 10∙5 = 162 liczby.
po których przychodzi 5 liczb postaci
Dla każdej cyfry
c = 1, 2, 3, 4, 5, 6, 7, 8
wypiszemy w ten sposób 14 liczb. To łącznie daje
8∙14 = 112 liczb. Następnie wypisujemy liczby zaczynające się od dziewiątki. Warunek
mówiący, że w zapisie liczby występuje dziewiątka, jest teraz spełniony; na drugim miejscu
może zatem wystąpić dowolna z 10 cyfr, a na trzecim dowolna z pięciu cyfr nieparzystych:
1, 2, 5, 7, 9. To daje łącznie 50 liczb, a więc ostatecznie dostajemy 162 liczby.
Komentarz
Zdający mogą próbować wypisywać liczby w różnej kolejności, stosując różne strategie.
W przypadku gdy zdający wyłącznie wypisuje liczby i podaje ostateczną odpowiedź,
uznajemy tylko rozwiązania całkowicie bezbłędne: odpowiedź 162 popartą poprawną listą
liczb. Za takie rozwiązanie zdający powinien otrzymać 5 punktów. Za rozwiązania
polegające na wypisywaniu liczb, niezawierające wyjaśnień i prowadzące do błędnej
odpowiedzi zdający powinien otrzymać 0 punktów. Jeśli zdający poda odpowiedź poprawną
(162 liczby) bez jakiegokolwiek uzasadnienia, to za takie rozwiązanie można otrzymać co
najwyżej 1 punkt. Jeśli natomiast poprawna odpowiedź jest poparta nieprawidłową listą
liczb, to zdający otrzymuje 0 punktów.
Metoda polegająca na wypisywaniu liczb może – jak widzieliśmy wyżej – prowadzić do
trafnych uogólnień. Pokonanie zasadniczych trudności zadania polega na dokonaniu dwóch
obserwacji: dla każdej cyfry różnej od 0 i 9 mamy 14 interesujących nas liczb zaczynających
się tą cyfrą oraz dla cyfry 9 mamy 50 liczb zaczynających się tą cyfrą.
Schemat oceniania VI sposobu rozwiązania
Jeśli zdający opisze regułę prowadzącą do wypisania poprawnej listy, to przyznajemy punkty
według następującego schematu:
Istotny postęp 2 pkt
- Zdający zauważy, że jeśli pierwsza cyfra jest różna od 9, to mamy 14 liczb lub
- zdający zauważy, że jeśli pierwsza cyfra jest dziewiątką, to mamy 50 liczb.
Pokonanie zasadniczych trudności 4 pkt
Zdający zauważy obie reguły opisane w poprzedniej kategorii.
Rozwiązanie pełne 5 pkt
Zdający pokona zasadnicze trudności zadania i ponadto poprawnie obliczy liczbę wszystkich
rozważanych liczb:
8∙14 + 50 = 162.
Uwaga
W tej metodzie rozwiązania zdający może popełnić wiele błędów. Na przykład może,
wypisując liczby zaczynające się cyfrą 1, nie zauważyć, że liczba 199 pojawia się dwukrotnie:
raz w ciągu 10 liczb
109, 119, 129, 139, 149, 159, 169, 179, 189, 199
i drugi raz w ciągu liczb
191, 193, 195, 197, 199.
Jeśli zdający wyłącznie zauważy, że istnieje 15 liczb zaczynających się od cyfry różnej od 9,
powinien otrzymać 1 punkt. Inny błąd może polegać na złym obliczeniu, ile jest liczb
zaczynających się od dziewiątki. Zdający może na przykład zapomnieć, że rozważamy
wyłącznie liczby nieparzyste i przyjmie, że istnieje 100 takich liczb. Za taką obserwację też
powinien otrzymać 1 punkt. Te błędy mogą prowadzić do następujących błędnych
odpowiedzi:
8∙15 + 50 = 170
oraz
8∙14 + 100 = 192
Za doprowadzenie rozwiązania do końca z jednym z tych dwóch błędów zdający powinien
otrzymać 4 punkty. Oba opisane błędy prowadzą do odpowiedzi
8∙15 + 100 = 220,
za którą zdający powinien otrzymać 3 punkty.