Odpowiedź:
Sposób I (pierwsza pochodna)
Definiujemy funkcję
ƒ
określoną wzorem
Funkcja
ƒ
jest różniczkowalna, obliczamy pochodną funkcji:
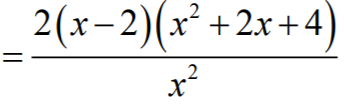
Ponieważ 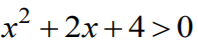 dla każdej liczby rzeczywistej x, to
dla każdej liczby rzeczywistej x, to
ƒ'(x) = 0 wtedy i tylko wtedy, gdy
x = 2
ƒ'(x) < 0 wtedy i tylko wtedy, gdy
x∈(0,2)
ƒ'(x) > 0 wtedy i tylko wtedy, gdy
x∈ (2, +∞)
Wynika stąd, że funkcja
ƒ
jest malejąca w przedziale (0,2⟩
i jest rosnąca w przedziale
⟨2, +∞) , czyli dla
x = 2
przyjmuje wartość najmniejszą.
Obliczamy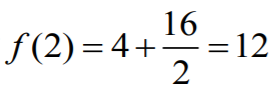 , stąd wynika, że
ƒ(x) ≥ 12 co należało udowodnić.
, stąd wynika, że
ƒ(x) ≥ 12 co należało udowodnić.
Schemat oceniania I sposobu rozwiązania
Rozwiązanie, w którym jest istotny postęp 1 pkt
Określenie funkcji 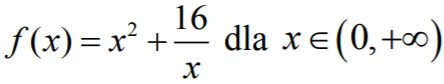 i obliczenie jej pochodnej
i obliczenie jej pochodnej
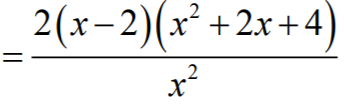
Pokonanie zasadniczych trudności 2 pkt
Obliczenie miejsca zerowego pochodnej i wyznaczenie przedziałów, w których pochodna ma
„stały znak”:
ƒ'(x) = 0 wtedy i tylko wtedy, gdy x = 2
ƒ'(x) < 0 wtedy i tylko wtedy, gdy x∈(0,2)
ƒ'(x) > 0 wtedy i tylko wtedy, gdy x∈ (2, +∞)
Rozwiązanie pełne 3 pkt
Stwierdzenie, że funkcja ƒ jest malejąca w przedziale (0,2⟩ i jest rosnąca w przedziale ⟨2, +∞), czyli dla
x = 2
przyjmuje wartość najmniejszą.
Obliczenie ƒ(2) = 12 i zapisanie wniosku: ƒ(x) ≥ 12, co należało udowodnić.
Uwagi
1. Zdający po obliczeniu, że ƒ'(x) = 0 tylko dla
x = 2, może uzasadnić tezę korzystając
z drugiej pochodnej funkcji ƒ.
2. Jeżeli zdający obliczy, że ƒ'(x) = 0 tylko dla x = 2 i stąd już wywnioskuje fakt: ƒ(x) ≥ ƒ(2) = 12, to za rozwiązanie przyznajemy 2 punkty.
Komentarz
Jeżeli w obliczaniu pochodnej zdający popełni błąd, który nie zmieni miejsc zerowych
pochodnej i dalej doprowadzi rozwiązanie do końca, to może otrzymać za całe zadanie
maksymalnie 2 punkty.
Przykłady tego typu błędów:
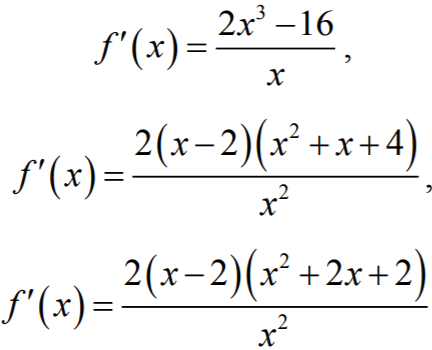
Jeżeli w obliczaniu pochodnej zdający popełni błąd, który zmienia miejsca zerowe pochodnej,
to otrzymuje za zadanie 0 punktów.
Sposób II (przekształcenia równoważne)
Zapisujemy nierówność 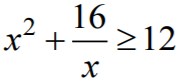 i przekształcamy ją równoważnie:
i przekształcamy ją równoważnie:
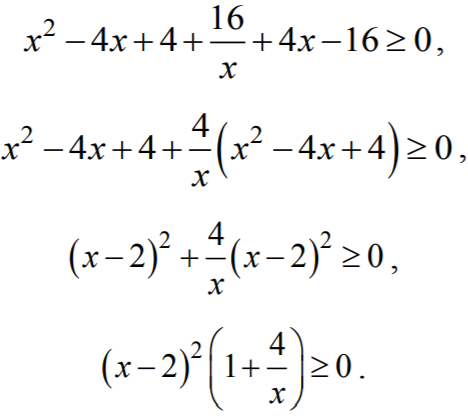
Jeżeli
x > 0
, to lewa strona nierówności jest nieujemna, jako iloczyn czynników nieujemnego
i dodatniego, co należało udowodnić.
Schemat oceniania II sposobu rozwiązania
Rozwiązanie, w którym jest istotny postęp 1 pkt
Zapisanie nierówności w postaci 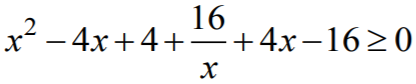 .
.
Pokonanie zasadniczych trudności 2 pkt
Zapisanie nierówności w postaci 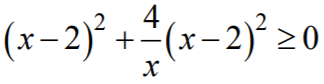
Rozwiązanie pełne 4 pkt
- Zapisanie nierówności w postaci
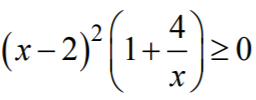 i stwierdzenie, że jeżeli
x > 0
, to
lewa strona nierówności jest nieujemna, bo iloczyn czynników nieujemnego
i dodatniego jest nieujemny, co kończy dowód
i stwierdzenie, że jeżeli
x > 0
, to
lewa strona nierówności jest nieujemna, bo iloczyn czynników nieujemnego
i dodatniego jest nieujemny, co kończy dowód
albo
- zapisanie nierówności w postaci
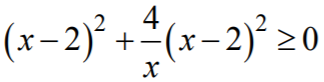 i stwierdzenie, że jeżeli
x > 0 ,
to lewa strona nierówności jest nieujemna, bo suma dwóch liczb nieujemnych jest
nieujemna, co kończy dowód.
i stwierdzenie, że jeżeli
x > 0 ,
to lewa strona nierówności jest nieujemna, bo suma dwóch liczb nieujemnych jest
nieujemna, co kończy dowód.
Sposób III (funkcja wymierna)
Zapisujemy nierówność 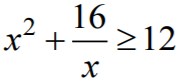 w postaci równoważnej
w postaci równoważnej 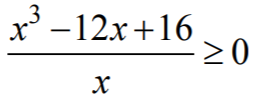 .
Przy założeniu
x > 0
, nierówność ta jest równoważna nierówności
.
Przy założeniu
x > 0
, nierówność ta jest równoważna nierówności 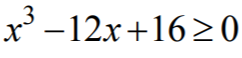 dla
x > 0.
dla
x > 0.
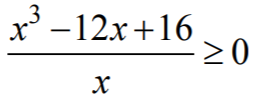 .
Przy założeniu
x > 0
, nierówność ta jest równoważna nierówności
.
Przy założeniu
x > 0
, nierówność ta jest równoważna nierówności Określamy wielomian
Stwierdzamy, że jednym z miejsc zerowych wielomianu
W
jest liczba
2. Po podzieleniu
wielomianu
W
przez dwumian
x – 2
otrzymujemy iloraz 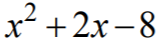 , który zapisujemy
w postaci iloczynowej
, który zapisujemy
w postaci iloczynowej 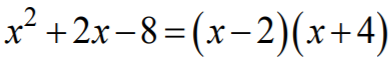 .
.
Stąd
Stwierdzamy, że jeżeli
x > 0
, to
W(x) ≥ 0 jako iloczyn czynników nieujemnych, co kończy
dowód.
Schemat oceniania III sposobu rozwiązania
Rozwiązanie, w którym jest istotny postęp 1 pkt
Stwierdzenie, że przy założeniu
x > 0
, nierówność jest równoważna nierówności 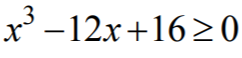 dla x > 0.
dla x > 0.
Pokonanie zasadniczych trudności 2 pkt
Zapisanie wielomianu
W
w postaci iloczynowej 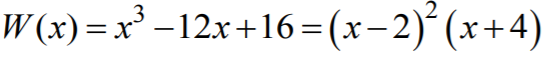
Rozwiązanie pełne 3 pkt
Uzasadnienie, że jeżeli
x > 0 , to
W(x) ≥ 0 co kończy dowód
Sposób IV (zastosowanie nierówności dla średniej arytmetycznej i geometrycznej)
Niektórzy zdający mogą odwołać się do tej nierówności, choć nie ma jej w podstawie
programowej i, jak widzieliśmy, rozwiązanie zadania nie wymaga jej znajomości.
Rozumowanie przebiega tak.
Lewą stronę nierówności zapisujemy w postaci
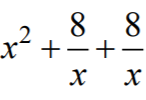
Przy założeniu
x > 0
, korzystamy z nierówności dla średniej arytmetycznej i średniej
geometrycznej:
jeżeli
a > 0, b > 0, c > 0
, to
Podstawiając
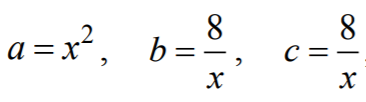
otrzymujemy
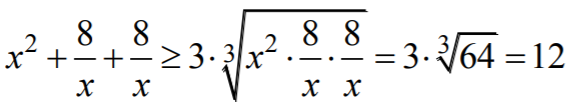
Stąd wynika, że 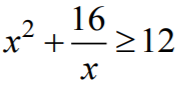 , co kończy dowód.
, co kończy dowód.
Schemat oceniania IV sposobu rozwiązania
Rozwiązanie, w którym postęp jest wprawdzie niewielki, ale konieczny na drodze do
pełnego rozwiązania zadania 1 pkt
Zapisanie lewej strony nierówności w postaci 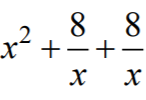
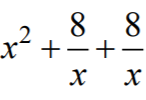
Pokonanie zasadniczych trudności 2 pkt
Zastosowanie nierówności dla średniej arytmetycznej i średniej geometrycznej:
jeżeli a > 0, b > 0, c > 0 , to
Rozwiązanie pełne 3 pkt
Zapisanie, że dla
x > 0
, po zastosowaniu nierówności dla średniej arytmetycznej i średniej
geometrycznej otrzymujemy 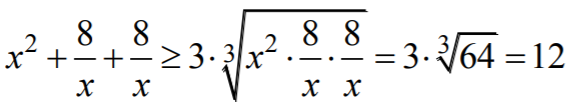 , co kończy dowód.
, co kończy dowód.
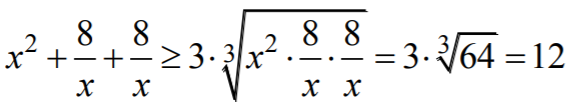 , co kończy dowód.
, co kończy dowód.