Odpowiedź:
Oznaczmy literą x długość boku kwadratowych naroży. Podstawa pudełka ma wymiary
(80 − 2x)×(50 − 2x)
Wysokość pudełka jest równa x. Zatem objętość wyraża się wzorem
V = (80 − 2x)·(50 − 2x)·x,
czyli
V = (4000 − 160x − 100x + 4x2)·x = 4x3 − 260x2 + 4000x = 4(x3 − 65x2 + 1000x)
dla 0 < x < 25
Rozważmy funkcję
ƒ(x) = x3 − 65x2 + 1000x określoną dla każdej liczby rzeczywistej x.
Obliczamy pochodną tej funkcji:
ƒ'(x) = 3x2 − 130x + 1000
Następnie znajdujemy miejsca zerowe tej pochodnej:
∆ = 1302 − 12·1000 = 16900 −12000 = 4900,
Ponadto
ƒ'(x) > 0 w każdym z przedziałów 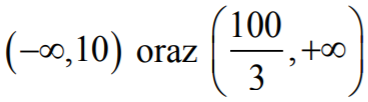
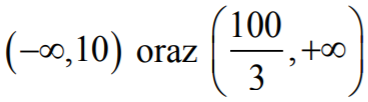
oraz
ƒ'(x) < 0 w przedziale 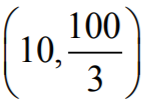
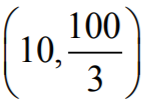
Zatem funkcja ƒ jest rosnąca w każdym z przedziałów 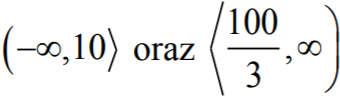 i malejąca
w przedziale
i malejąca
w przedziale 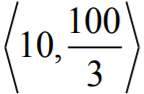 .
.
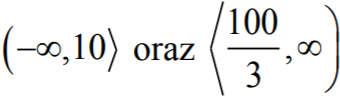 i malejąca
w przedziale
i malejąca
w przedziale V = (80 − 20)·(50 − 20)·10 = 18000 cm2
Schemat oceniania
Rozwiązanie zadania składa się z trzech etapów.
a) Pierwszy etap (3 pkt) składa się z trzech części:
- wybór zmiennej i wyrażenie za pomocą tej zmiennej wielkości, które będą potrzebne do zdefiniowania funkcji. Oznaczenie literą x długości boku kwadratowych naroży, zapisanie wymiarów podstawy pudełka
(80 − 2x)×(50 − 2x)
- zdefiniowanie funkcji jednej zmiennej, zapisanie objętości jako funkcji zmiennej wysokości pudełka x:
V = (80 − 2x)·(50 − 2x)·x
- określenie dziedziny funkcji V:
0 < x < 25
Zdający otrzymuje 2 punkty za poprawne zdefiniowanie funkcji zmiennej x opisującej
objętość prostopadłościanu. Ponadto zdający otrzymuje 1 punkt za poprawne określenie
dziedziny wynikającej z treści zadania, a nie z wyznaczonego wzoru funkcji.
b) Drugi etap (3 pkt) składa się z trzech części:
- wyznaczenie pochodnej funkcji ƒ:
ƒ'(x) = 3x2 − 130x + 1000
- obliczenie miejsc zerowych pochodnej:
- uzasadnienie (np. przez badanie monotoniczności funkcji), że funkcja posiada wartość największą w punkcie x =10 .
c) Trzeci etap (1 pkt).
Obliczenie największej objętości:
V = (80 − 20)·(50 − 20)·10 = 18000 cm2
Komentarz
Zdający rozwiązując zadanie może nie doprowadzić rozumowania do końca lub popełnić
różnego rodzaju błędy np.:
1. Błędne określenie dziedziny funkcji V np. zapisanie
x > 0
lub
x < 50
. Jeżeli zdający nie
poda dziedziny funkcji lub poda ją błędnie, to za całe rozwiązanie może otrzymać
maksymalnie 6 punktów.
2. Błędne zapisanie wzoru na objętość pudełka (np. niewłaściwe określenie wymiarów
pudełka lub wzoru na objętość prostopadłościanu).
3. Niewłaściwe wyznaczenie pochodnej rozważanej funkcji.
4. Nieprawidłowo obliczone miejsca zerowe pochodnej.
5. Błędne określenie monotoniczności funkcji oraz jej ekstremów.
6. Brak uzasadnienia, błędne lub niepełne uzasadnienie, że funkcja V w punkcie
x =10
przyjmuje maksimum lokalne.
7. Nieobliczenie lub błędne obliczenie największej objętości pudełka.
Schemat oceniania pokazuje jak w poszczególnych sytuacjach ocenić rozwiązanie zadania.