Odpowiedź:
Przykładowe pełne rozwiązania
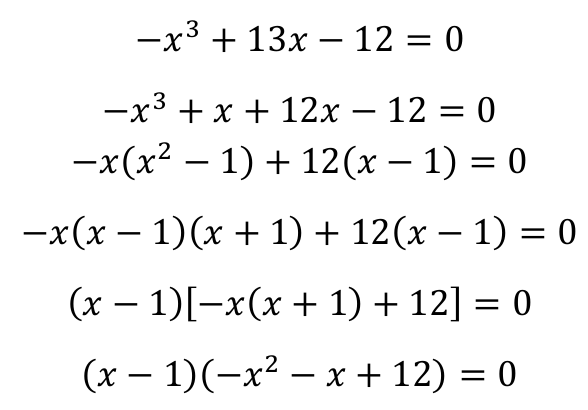
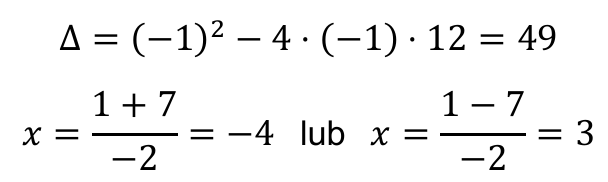
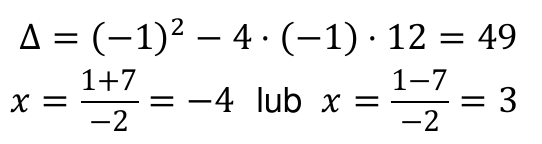
Przekształcamy lewą stronę równania
−x3 + 13x − 12 = 0
w sposób równoważny tak, aby otrzymać postać iloczynową wielomianu
−x3 + 13x − 12:
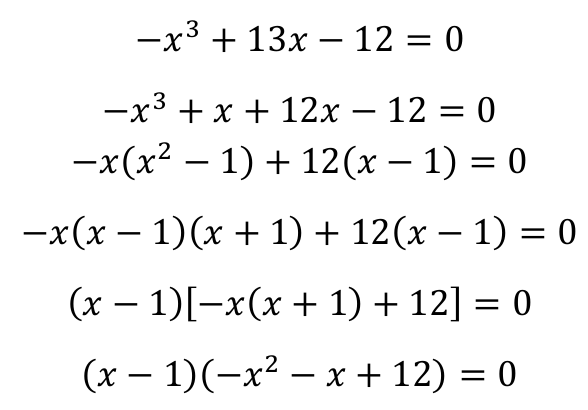
Korzystamy z własności iloczynu i zapisujemy równanie
(x − 1)(−x2 − x + 12) = 0
jako alternatywę równań:
x − 1= 0
lub
− x2 − x + 12 = 0
Rozwiązując równanie x − 1 = 0, otrzymujemy: x = 1
Rozwiązując równanie kwadratowe, otrzymamy:
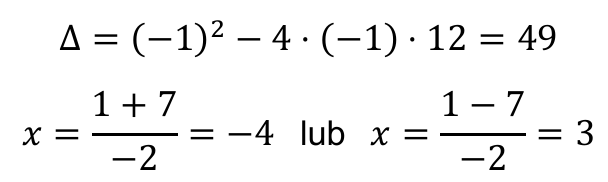
Zatem rozwiązaniami równania są liczby: (−4), 1 oraz 3.
Sposób II
Korzystamy z definicji podzielności wielomianu W(x) przez dwumian (x − a).
Obliczamy W(1) = 0 i stwierdzamy, że liczba 1 jest pierwiastkiem wielomianu
W(x) = −x3 + 13x − 12 = 0
Po podzieleniu wielomianu W przez dwumian (x − 1) otrzymujemy iloraz
(−x2 − x + 12).
Zapisujemy dane równanie w postaci
(x − 1)(−x2 − x + 12) = 0
Stąd
x − 1 = 0 lub −x2 − x + 12 = 0
Rozwiązując równanie kwadratowe, otrzymamy:
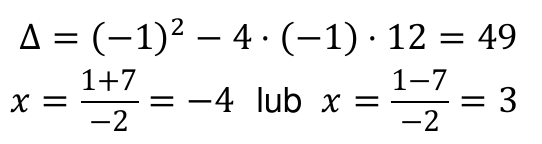
Rozwiązując równanie x − 1 = 0, otrzymujemy: x = 1
Rozwiązania równania to: x = −4 lub x = 1 lub x = 3.
schemat punktacji
3 pkt – obliczenie i zapisanie rozwiązań równania: (−4), 1, 3
2 pkt – zapisanie alternatywy równań: x − 1 = 0 lub −x2 − x + 12 = 0
1 pkt – poprawne przekształcenie równania do postaci (x − 1)(−x2 − x + 12) = 0
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.