Odpowiedź:
Przykładowe pełne rozwiązanie
Niech m będzie liczbą dni potrzebnych na rozwiązanie pozostałych zadań.
Szymonowi pozostało do rozwiązania 3697 − 97 = 3600 zadań, zatem
m ⋅ n = 3600
Przy zwiększonej dziennej liczbie rozwiązanych zadań otrzymujemy równanie:
(m − 10) ⋅ (n + 5) = 3600
mn + 5m − 10n − 50 = 3600
Podstawiamy mn = 3600 i wyznaczamy wielkość n:
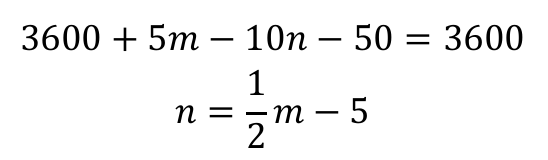
Podstawiając
do równania kwadratowego otrzymujemy:
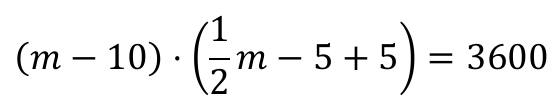
Opuszczając nawiasy i przekształcając równanie, otrzymujemy:
m2 − 10m − 7200 = 0
Wyróżnikiem tego równania kwadratowego jest Δ = 28900 , zaś jego rozwiązania to m1 = −80 oraz m2 = 90. Z warunków zadania wynika, że jedynym rozwiązaniem zadania jest liczba 90.
Szymon zamierza rozwiązywać codziennie 40 zadań. Zajmie mu to 90 dni.
schemat punktacji
4 pkt – rozwiązanie równania i podanie prawidłowego wyniku: m = 90
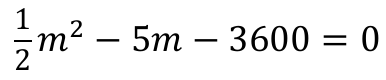
3 pkt – zapisanie równania z jedną niewiadomą:
lub 2n2 + 10n − 3600 = 0
2 pkt – zapisanie równania uwzględniającego warunki zadania: (m − 10) ⋅ (n + 5) = 3600
lub mn + 5m − 10n − 50 = 3600 oraz wyznaczenie wielkości m lub n:
n=½ m − 5 lub m = 2n + 10
1 pkt – zapisanie, że do rozwiązania pozostało 3600 zadań i zapisanie równania m ⋅ n = 3600
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.