Odpowiedź:
Przykładowe pełne rozwiązania



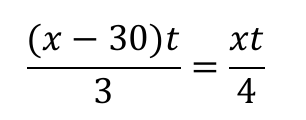
Sposób I
W czasie, gdy pies pokonuje dystans 4 m, wykonując dwa skoki, lis pokonuje 3 m.
Zatem po każdym cyklu dystans między zwierzętami zmniejsza się o 1 m. Wynika z tego,
że dystans 30 m zostanie zniwelowany po 30 cyklach. W tym czasie lis przebiegnie
30 ⋅ 3 = 90 metrów, a pies 30 ⋅ 4 = 120 metrów.
Sposób II
Niech t oznacza czas, w którym pies skacze dwa razy, więc przebywa drogę długości
4 m. W tym czasie lis przebywa drogę długości 3 m. Niech vp oznacza prędkość psa,
a vl – prędkość lisa.
Zachodzą więc równości

Jeśli przez T oznaczymy czas, po jakim pies dogoni lisa, zaś przez x dystans, który przebiegnie pies, mamy zależności czasu dla obu zwierząt.
Dla lisa:

Dla psa:

Przyrównując obie wielkości, otrzymujemy równanie:
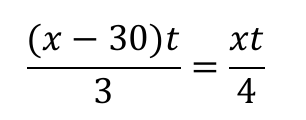
Z warunków zadania wynika, że t ≠ 0 , zatem możemy przekształcić to równanie do postaci
4(x − 30) = 3x
Rozwiązaniem tego równania jest x = 120.
Pies przebiegnie dystans 120 metrów.
schemat punktacji
3 pkt – obliczenie dystansu, jaki pokona pies: 120 m.
2 pkt – ustalenie, że musi się odbyć 30 cykli,
ALBO
zapisanie równania
1 pkt – ustalenie, że w jednym cyklu różnica odległości między zwierzętami zmniejsza się o 1 m,
ALBO wyznaczenie prędkości obu zwierząt
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.