Odpowiedź:
Przykładowe pełne rozwiązania
Sposób I
Punkt przecięcia osi symetrii funkcji kwadratowej z osią Ox jest środkiem odcinka łączącego jej miejsca zerowe, zatem
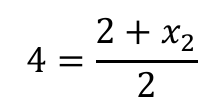
Stąd x2 = 6.
Obliczamy współczynnik a funkcji, zapisując postać iloczynową funkcji z podstawionymi wartościami x1 , x2 oraz współrzędnymi punktu (0, 8):
8 = a(0 − 2)(0 − 6)
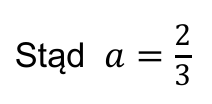
Postać iloczynowa szukanej funkcji to
Sposób II
Ponieważ osią symetrii szukanej funkcji kwadratowej jest prosta x = 4, możemy stwierdzić, że pierwsza współrzędna wierzchołka paraboli będącej jej wykresem to p = 4. Postać kanoniczna tej funkcji to
Do wykresu funkcji należą dwa punkty: (0, 8) oraz (2, 0). Podstawiając ich współrzędne do powyższego wzoru, otrzymujemy układ równań:
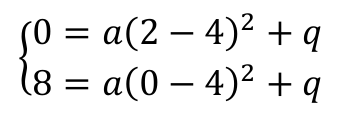
Rozwiązaniem tego układu są liczby
Możemy zapisać postać kanoniczną szukanej funkcji:
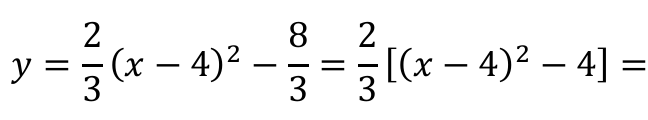
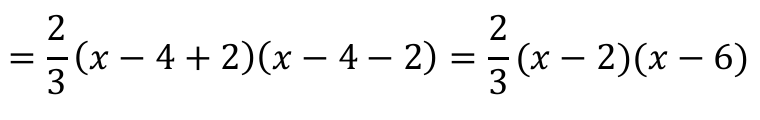
schemat punktacji
2 pkt – obliczenie współczynnika a i zapisanie funkcji w postaci iloczynowej:
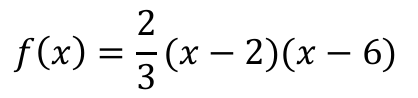
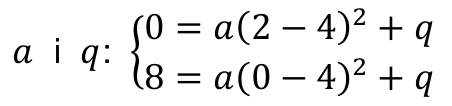
1 pkt – obliczenie drugiego miejsca zerowego: x2 = 6
ALBO
zapisanie układu równań pozwalającego obliczyć
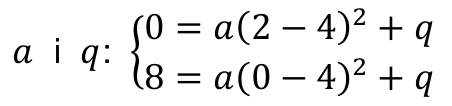
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.