Odpowiedź:
Przykładowe pełne rozwiązania
Sposób I
Trzy liczby, tworzące ciąg arytmetyczny o różnicy r, oznaczmy przez
b − r, b, b + r.
Zapisując warunek na sumę tego ciągu, możemy zauważyć, że
(b − r) + b + (b + r) = 24
3b = 24
b=8
Zatem ciąg arytmetyczny ma postać:
(8 − r, 8, 8 + r).
Po dodaniu kolejno do jego wyrazów liczb 4, 10, 40, otrzymujemy ciąg geometryczny:
(12 − r, 18, 48 + r)
Korzystając z własności ciągu geometrycznego, zapisujemy równanie:
182 = (12 − r) ⋅ (48 + r)
Po uproszczeniu otrzymujemy równanie kwadratowe
r2 + 36r − 252 = 0
Posiada ono dwa rozwiązania: (−42) oraz 6.
Gdy r = −42, wówczas szukanym ciągiem arytmetycznym jest (50, 8, −34).
W przypadku, gdy r = 6, mamy ciąg arytmetyczny (2, 8, 14).
Sposób II
Niech (an) będzie ciągiem arytmetycznym o różnicy r . Wtedy sumę tego ciągu możemy
zapisać jako
a1 + (a1 + r) + (a1 + 2r) = 24
Mamy stąd zależność
a1 = 8 − r
Z warunków zadania mamy, że liczby
a1 + 4, a1 + r + 10, a1 + 2r + 40
tworzą ciąg geometryczny. Korzystając z jego własności, otrzymujemy kolejną zależność:
(a1 + r + 10)2 = (a1 + 4) ⋅ (a1 + 2r + 40)
Po podstawieniu
a1 = 8 − r
otrzymujemy
182 = (12 − r) ⋅ (48 + r)
Po uproszczeniu otrzymujemy równanie kwadratowe
r2 + 36r − 252 = 0
Posiada ono dwa rozwiązania: (−42) oraz 6.
Gdy r = −42, wówczas a1 = 50, zaś kolejne liczby tego ciągu to 8 i (−34).
W przypadku, gdy r = 6, mamy a1 = 2, a kolejne wyrazy ciągu to 8 i 14 .
Szukanymi ciągami są: (50, 8, −34) oraz (2, 8, 14).
schemat punktacji
4 pkt – zapisanie dwóch ciągów: (50, 8, −34) oraz (2, 8, 14)
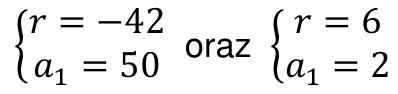
3 pkt – rozwiązanie układu równań:
ALBO
zapisanie jednego z dwóch ciągów: (50, 8, −34) albo (2, 8, 14)
2 pkt – obliczenie środkowego wyrazu ciągu arytmetycznego: b = 8
ALBO
zapisanie warunków na sumę ciągu arytmetycznego i warunku ciągu geometrycznego:
a1 + (a1 + r) + (a1 + 2r) = 24 oraz
(a1 + r + 10)2 = (a1 + 4) ⋅ (a1 + 2r + 40)
1 pkt – zapisanie warunku na sumę ciągu arytmetycznego:
(b − r) + b + (b + r) = 24 lub a1 + (a1 + r) + (a1 + 2r) = 24
ALBO
zapisanie warunku ciągu geometrycznego:
(a1 + r + 10)2 = (a 1 + 4) ⋅ (a1 + 2r + 40)
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.