Odpowiedź:
Przykładowe pełne rozwiązanie
Niech 𝛼 = |∡𝐵𝐴𝐶|.
Ponieważ 𝑃Δ𝐴𝐷𝐸 = 2 ⋅ 𝑃Δ𝐴𝐵𝐶 oraz
𝑃Δ𝐴𝐵𝐶 = ½ |𝐴𝐵| ∙ |𝐴𝐶| ∙ sin 𝛼
i 𝑃Δ𝐴𝐷𝐸 = ½ |𝐴𝐷| ∙ |𝐴𝐸| ∙ sin 𝛼,
zatem mamy
½ |𝐴𝐷| ∙ |𝐴𝐸| ∙ sin 𝛼 = 2 ∙ ½ |𝐴𝐵| ∙ |𝐴𝐶| ∙ sin 𝛼
Stąd
|𝐴𝐷| ∙ |𝐴𝐸| = 2 ∙ |𝐴𝐵| ∙ |𝐴𝐶|
Po wstawieniu długości boków |𝐴𝐵| = 24, |𝐴𝐶| = 10 mamy
|𝐴𝐷| ∙ |𝐴𝐸| = 2 ∙ 24 ∙ 10
|𝐴𝐷| ∙ |𝐴𝐸| = 480
Stosując twierdzenie o dwusiecznej dla trójkąta 𝐴𝐷𝐸, otrzymujemy:
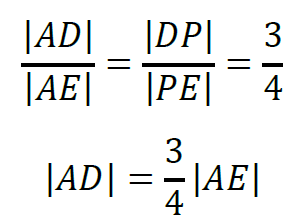
Uwzględniając obie te zależności, otrzymujemy:
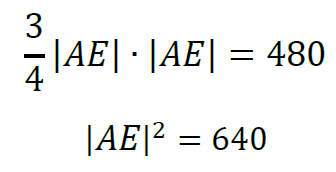
Zatem
oraz
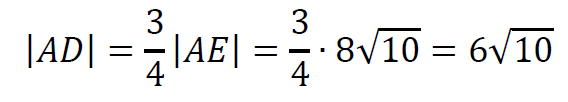
schemat punktacji
2 pkt – zastosowanie poprawnej metody obliczenia długości boków 𝐴𝐷, 𝐴𝐸 oraz podanie wyników: |𝐴𝐸| = 8√10, |𝐴𝐷| = 6√10
1 pkt – wyznaczenie i zapisanie zależności pomiędzy długościami dwóch boków trójkąta
𝐴𝐷𝐸 : |𝐴𝐷| ∙ |𝐴𝐸| = 480
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.