Odpowiedź:
Przykładowe pełne rozwiązania
Sposób I
Niech 𝛼 = |∡𝐵𝐴𝐶|. Wiemy, że
Stąd
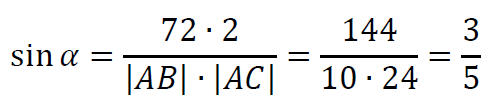
Ponieważ cosinus kąta ostrego jest dodatni, korzystając z jedynki trygonometrycznej, obliczamy
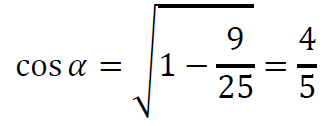
Z twierdzenia cosinusów mamy
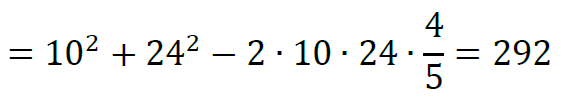
Zatem długość odcinka 𝐵𝐶 jest równa
Sposób II
Niech ℎ będzie wysokością trójkąta 𝐴𝐵𝐶 opuszczoną z wierzchołka 𝐶, punkt 𝐹 – jej spodkiem, a 𝑥 – długością odcinka 𝐴𝐹 (zobacz rysunek).
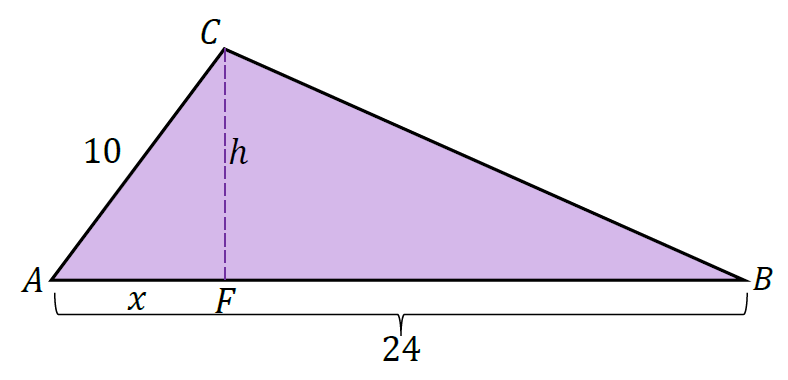
Ze wzoru na pole trójkąta 𝐴𝐵𝐶 otrzymujemy równanie:
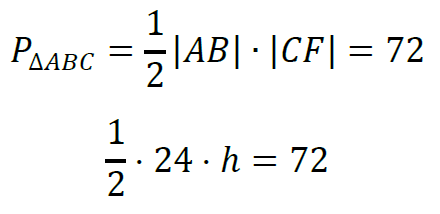
Stąd ℎ = 6.
Korzystając z twierdzenia Pitagorasa dla trójkąta 𝐴𝐹𝐶, mamy:
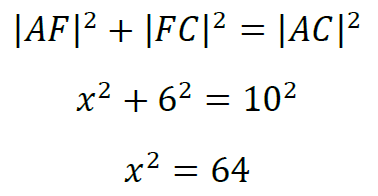
Zatem długość odcinka 𝐴𝐹 jest równa 8.
Obliczamy długość odcinka 𝐹𝐵:
|𝐹𝐵| = 24 − 8 = 16
Korzystając z twierdzenia Pitagorasa dla trójkąta 𝐴𝐹𝐶, mamy:
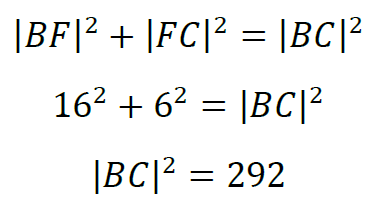
Zatem długość odcinka 𝐵𝐶 jest równa
schemat punktacji
3 pkt – zastosowanie poprawnej metody obliczenia długości boku 𝐵𝐶 i podanie
prawidłowego wyniku: |𝐵𝐶| = 2√73
2 pkt – obliczenie wartości cosinusa kąta przy wierzchołku 𝐴: cos 𝛼 = 4⁄5
i zastosowanie jej w twierdzeniu cosinusów do obliczenia długości boku 𝐵𝐶
|𝐵𝐶|2 = |𝐴𝐵|² + |𝐴𝐶|² − 2|𝐴𝐵| ∙ |𝐴𝐶| ∙ cos 𝛼
ALBO
obliczenie długości odcinka 𝐹𝐵 i zapisanie twierdzenia Pitagorasa dla trójkąta 𝐴𝐹𝐶.
1 pkt – obliczenie wartości sinusa kąta przy wierzchołku 𝐴: sin 𝛼 = 3⁄5
ALBO
obliczenie wysokości trójkąta 𝐴𝐵𝐶: ℎ = 6
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.