Odpowiedź:
Przykładowe pełne rozwiązania
Sposób I
Z warunku
wynika, że
|𝑄𝑅| = 3, więc |𝑆𝑅| = |𝑆𝑄| + |𝑄𝑅| = 1 + 3 = 4.
Stosując teraz twierdzenie Pitagorasa do trójkąta 𝑆𝑇𝑅, otrzymujemy kolejno
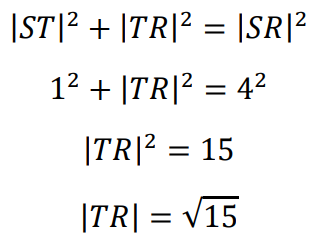
Ponieważ 𝑆𝑇 ∥ 𝑄𝑈, więc stosujemy twierdzenie Talesa i obliczamy |𝑇𝑈|:
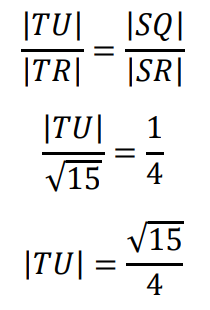
Sposób II
Ponieważ
i promień okręgu jest równy 1, więc:
|𝑃𝑄| = 2, |𝑄𝑅| = 3, |𝑃𝑅| = 5, |𝑆𝑅| = 4.
Stosujemy twierdzenie o stycznej i siecznej i obliczamy |𝑇𝑅|:
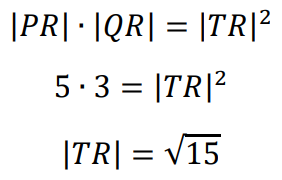
Trójkąt 𝑇𝑆𝑅 jest podobny do trójkąta 𝑈𝑄𝑅, ponieważ odcinki 𝑇𝑆 i 𝑈𝑄 są równoległe, a kąt przy wierzchołku 𝑅 jest wspólny. Z podobieństwa tych trójkątów wynika proporcjonalność długości odpowiednich boków tych trójkątów:
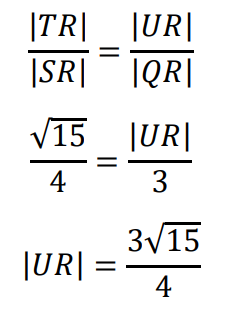
Zatem
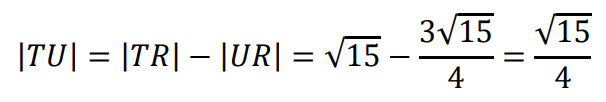
schemat punktacji
Dla rozwiązania sposobem I:
2 pkt – zastosowanie poprawnej metody obliczenia długości odcinka 𝑇𝑈 oraz podanie poprawnego wyniku:
1 pkt – zastosowanie twierdzenia Pitagorasa do trójkąta 𝑆𝑇𝑅, np. 1² + |𝑇𝑅|² = 4²
ALBO
zastosowanie twierdzenia Talesa do odcinków 𝑇𝑈, 𝑇𝑅, 𝑆𝑄, 𝑆𝑅, np.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.
Dla rozwiązania sposobem II:
2 pkt – zastosowanie poprawnej metody obliczenia długości odcinka 𝑇𝑈 oraz podanie poprawnego wyniku:
1 pkt – zastosowanie twierdzenia o stycznej i siecznej, np. 5 ∙ 3 = |𝑇𝑅|²
ALBO
zapisanie równania wynikającego z proporcjonalności długości boków 𝑇𝑅, 𝑆𝑅, 𝑈𝑅, 𝑄𝑅 trójkątów podobnych 𝑇𝑆𝑅 i 𝑈𝑄𝑅, np.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.