Odpowiedź:
Przykładowe pełne rozwiązanie
Niech 𝑟 oznacza promień koła i oznaczmy przez 𝑥 długość boku kwadratu.
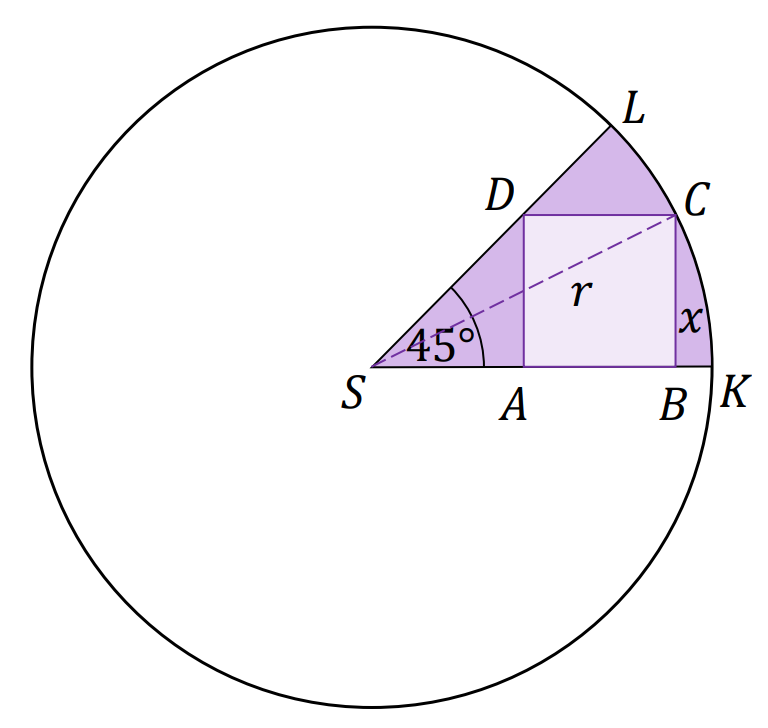
Ponieważ trójkąt 𝑆𝐴𝐷 jest prostokątny i równoramienny, więc |𝐴𝑆| = |𝐴𝐷| = 𝑥.
Stąd
|𝐵𝑆| = |𝐴𝐵| + |𝐴𝑆| = 2𝑥
Prowadzimy promień 𝑆𝐶 i otrzymujemy trójkąt prostokątny 𝑆𝐵𝐶, do którego stosujemy twierdzenie Pitagorasa i otrzymujemy:
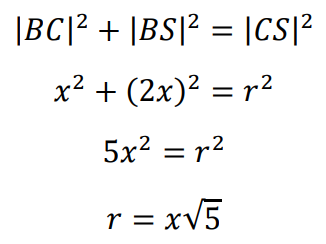
Wyznaczamy pole 𝑃𝐾𝑆𝐿 wycinka kołowego 𝐾𝑆𝐿 w zależności od 𝑥:
Obliczamy stosunek pola kwadratu do pola wycinka kołowego 𝐾𝑆𝐿:
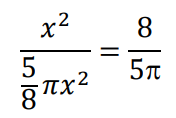
schemat punktacji
3 pkt – obliczenie stosunku pola kwadratu do pola wycinka kołowego:
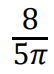
2 pkt – wyznaczenie zależności między promieniem okręgu 𝑟 i długością boku kwadratu 𝐴𝐵𝐶𝐷, np. 𝑟 = 𝑥√5
1 pkt – wyznaczenie długości odcinka 𝐴𝑆 lub długości odcinka 𝐵𝑆 w zależności od długości 𝑥 boku kwadratu 𝐴𝐵𝐶𝐷: |𝐴𝑆| = 𝑥 (lub |𝐵𝑆| = 2𝑥)
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.