Odpowiedź:
Przykładowe pełne rozwiązanie
Sposób I
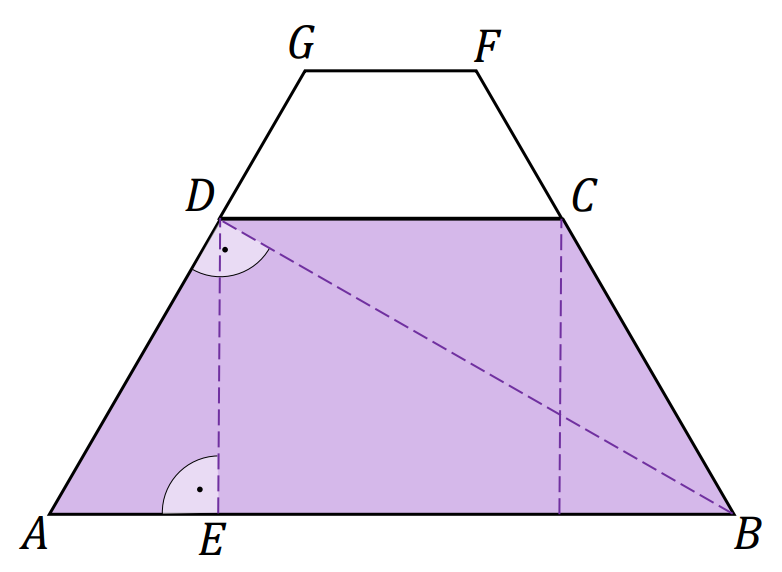
Opuszczamy z wierzchołka 𝐷 wysokość 𝐷𝐸 trapezu 𝐴𝐵𝐶𝐷. Korzystamy z własności trójkąta o kątach 30°, 60°, 90° i otrzymujemy:
|𝐴𝐵| = 12, |𝐵𝐷| = 6√3.
Korzystamy z własności trójkąta o kątach 30°, 60°, 90° i otrzymujemy:
|𝐴𝐸| = 3, |𝐷𝐸| = 3√3.
Obliczamy długość górnej podstawy trapezu 𝐴𝐵𝐶𝐷:
|𝐶𝐷| = |𝐴𝐵| − 2 ⋅ |𝐴𝐸| = 12 − 2 ⋅ 3 = 6
Trapezy 𝐶𝐷𝐹𝐺 i 𝐴𝐵𝐶𝐷 są podobne, więc skala 𝑘 podobieństwa jest równa stosunkowi długości dolnych podstaw tych trapezów:
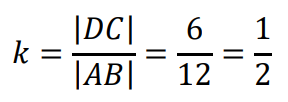
Korzystając z podobieństwa obu trapezów, obliczamy długość górnej podstawy trapezu 𝐷𝐶𝐹𝐺 oraz wysokość ℎ tego trapezu:
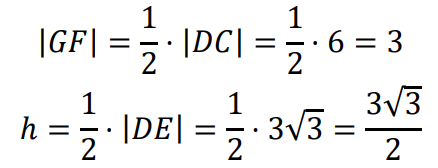
Obliczamy pole 𝑃𝐷𝐶𝐹𝐺 trapezu 𝐷𝐶𝐹𝐺:
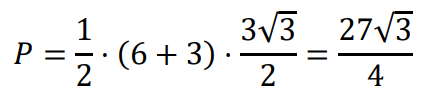
Sposób II
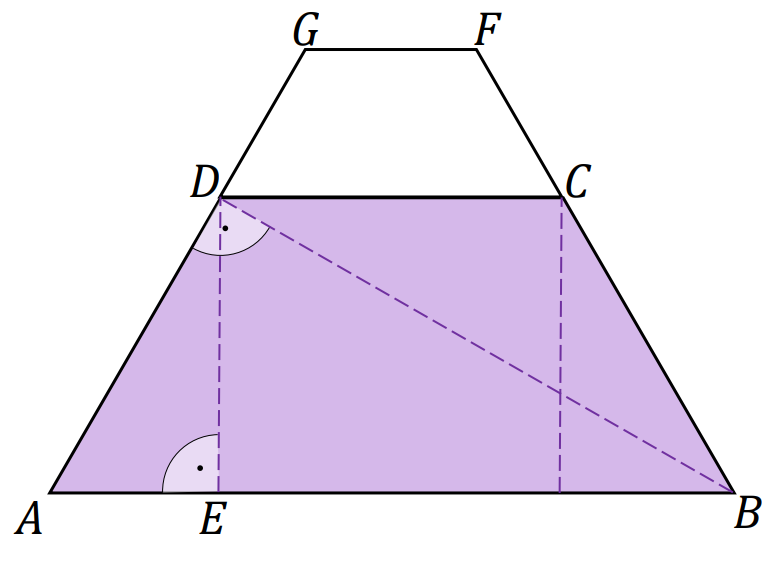
Opuszczamy z wierzchołka 𝐷 wysokość 𝐷𝐸 trapezu 𝐴𝐵𝐶𝐷. Korzystamy z własności trójkąta o kątach 30°, 60°, 90° i otrzymujemy |𝐴𝐵| = 12.
Korzystamy z własności trójkąta o kątach 30°, 60°, 90° i otrzymujemy:
|𝐴𝐸| = 3, |𝐷𝐸| = 3√3.
Obliczamy długość górnej podstawy trapezu 𝐴𝐵𝐶𝐷:
|𝐶𝐷| = |𝐴𝐵| − 2 ⋅ |𝐴𝐸| = 12 − 2 ⋅ 3 = 6
Trapezy 𝐶𝐷𝐹𝐺 i 𝐴𝐵𝐶𝐷 są podobne, więc skala 𝑘 podobieństwa jest równa stosunkowi długości dolnych podstaw tych trapezów:
Obliczamy pole 𝑃𝐴𝐵𝐶𝐷 trapezu 𝐴𝐵𝐶𝐷:
Korzystamy z twierdzenia o polach figur podobnych i obliczamy pole 𝑃𝐷𝐶𝐹𝐺 trapezu 𝐷𝐶𝐹𝐺:
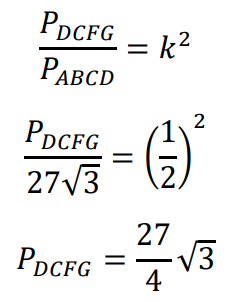
schemat punktacji
4 pkt – zastosowanie poprawnej metody obliczenia pola trapezu 𝐷𝐶𝐹𝐺 i zapisanie poprawnego wyniku:
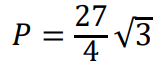
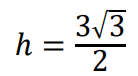
3 pkt – obliczenie długości podstawy 𝐹𝐺 trapezu 𝐷𝐶𝐹𝐺: |𝐹𝐺| = 3 oraz jego wysokości
ALBO
obliczenie skali podobieństwa trapezów: 𝑘 = ½
2 pkt – obliczenie skali podobieństwa trapezów: 𝑘 = ½
ALBO
obliczenie pola trapezu 𝐴𝐵𝐶𝐷: 27√3
1 pkt – obliczenie długości podstaw trapezu 𝐴𝐵𝐶𝐷: |𝐴𝐵| = 12, |𝐶𝐷| = 6 oraz jego wysokości 𝐻 = 3√3
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.