Odpowiedź:
Sposób I
Oznaczmy pole trapezu o podstawach 𝑎 i 𝑏 jako 𝑃1 oraz pole trapezu o podstawach 𝑏 i 𝑐 jako 𝑃2 (zobacz rysunki).
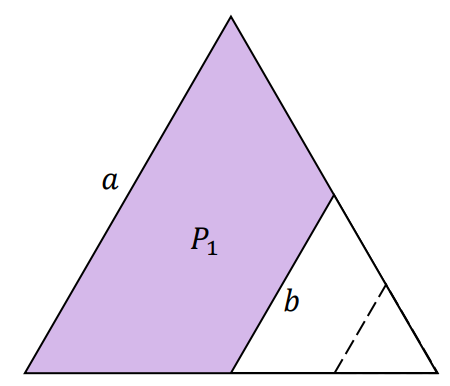
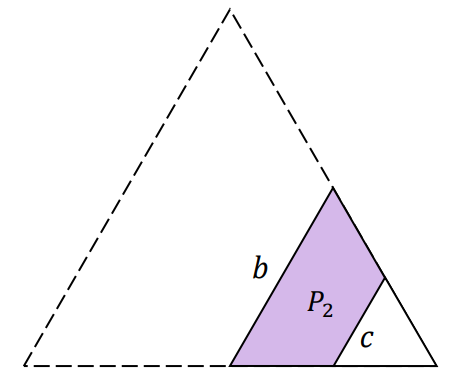
Pole 𝑃1 możemy zinterpretować jako różnicę pól trójkątów równobocznych o bokach 𝑎 i 𝑏:
Analogicznie pole 𝑃2 możemy zinterpretować jako różnicę pól trójkątów równobocznych o bokach 𝑏 i 𝑐:
Zatem stosunek pól będzie równy
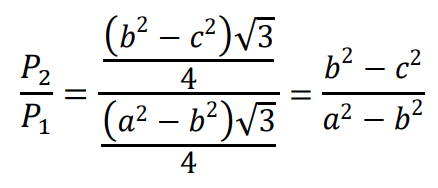
Sposób II
Dwie proste równoległe do jednego z boków trójkąta wyznaczają trójkąt równoboczny o boku długości 𝑏 oraz trójkąt równoboczny o boku długości 𝑐.
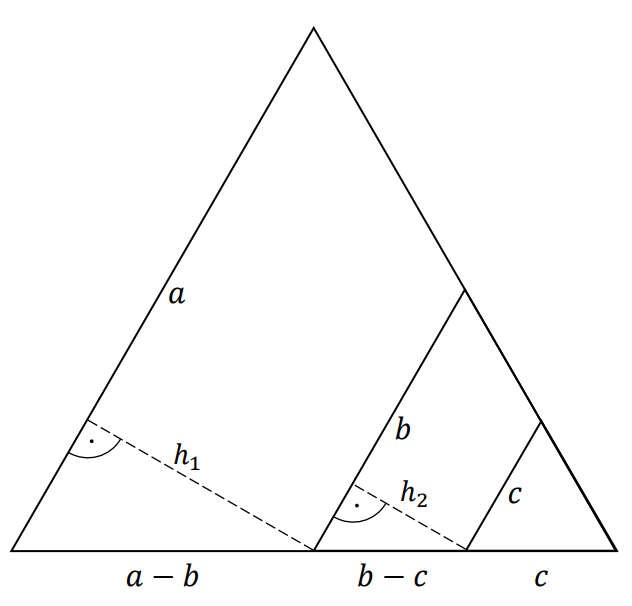
Możemy zatem stwierdzić, że ramiona otrzymanych trapezów mają długości odpowiednio (𝑎 − 𝑏) oraz (𝑏 − 𝑐).
Prowadzimy wysokość ℎ1 w trapezie o podstawach 𝑎 i 𝑏 oraz wysokość ℎ2 w trapezie o podstawach 𝑏 i 𝑐.
Korzystając z własności trójkąta o kątach 30°, 60°, 90°, wyznaczamy wysokości obu trapezów:
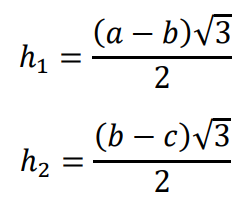
Niech 𝑃1 oznacza pole trapezu o podstawach 𝑎 i 𝑏, natomiast 𝑃2 – pole trapezu o podstawach 𝑏 i 𝑐. Wówczas
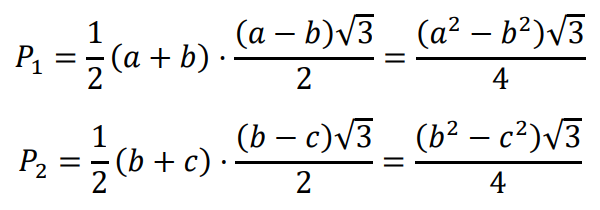
Wyznaczamy stosunek pól trapezów:
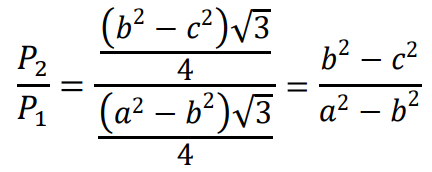
To należało pokazać.
schemat punktacji
2 pkt – spełnienie kryterium za 1 pkt zasad oceniania oraz wyznaczenie poprawnego stosunku pól trapezów:
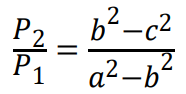
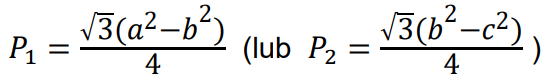
1 pkt – wyznaczenie pola 𝑃1 trapezu o podstawach 𝑎 i 𝑏 (lub pola 𝑃2 trapezu o podstawach 𝑏 i 𝑐):
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę lub brak rozwiązania.