Odpowiedź:
Przykładowe pełne rozwiązania
Sposób I
Wierzchołek 𝐷 równoległoboku 𝐴𝐵𝐶𝐷 jest punktem przecięcia prostych 𝐴𝐷 i 𝐶𝐷.
Obliczamy współczynniki kierunkowe prostych 𝐴𝐵 i 𝐵𝐶:
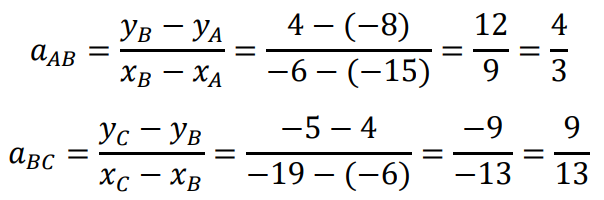
Ponieważ 𝐴𝐷 ∥ 𝐵𝐶, więc proste 𝐴𝐷 i 𝐵𝐶 mają równe wartości współczynników kierunkowych, tj. 𝑎𝐴𝐷 = 𝑎𝐵𝐶 = 9⁄13 . Wyznaczamy równanie prostej 𝐴𝐷:
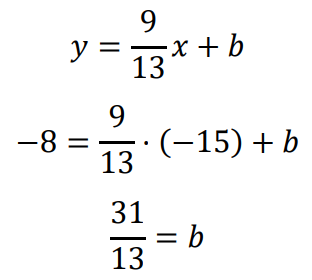
Zatem prosta 𝐴𝐷 ma równanie
Ponieważ 𝐷𝐶 ∥ 𝐴𝐵, więc proste 𝐷𝐶 i 𝐴𝐵 mają równe wartości współczynników kierunkowych, tj. 𝑎𝐷𝐶 = 𝑎𝐴𝐵 = 4⁄3 . Wyznaczamy równanie prostej 𝐷𝐶:
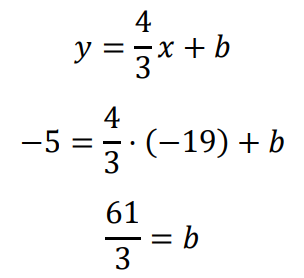
Zatem prosta 𝐷𝐶 ma równanie
Obliczamy współrzędne punktu przecięcia prostych 𝐴𝐷 i 𝐷𝐶:
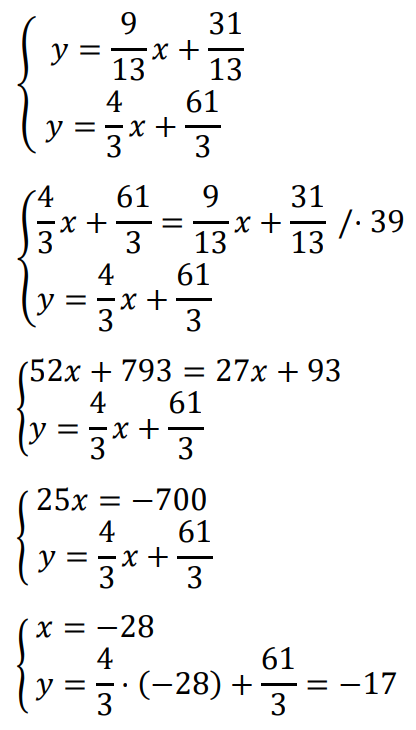
Wierzchołek 𝐷 ma współrzędne: 𝐷 = (−28, −17).
Sposób II
W równoległoboku 𝐴𝐵𝐶𝐷 przekątne dzielą się na połowy, a punkt 𝑆 przecięcia się przekątnych jest środkiem symetrii tego równoległoboku. Obliczamy współrzędne środka 𝑆 przekątnej 𝐴𝐶:
Ponieważ punkt 𝑆 jest środkiem symetrii równoległoboku, jest więc środkiem przekątnej 𝐵𝐷 tego równoległoboku. Obliczymy stąd współrzędne punktu 𝐷: Oznaczmy współrzędne punktu 𝐷 = (𝑥𝐷, 𝑦𝐷), wtedy
Stąd mamy:
Obliczamy 𝑥𝐷 oraz 𝑦𝐷:

Zatem punkt 𝐷 ma współrzędne: 𝐷 = (−28, −17).
schemat punktacji
3 pkt – obliczenie współrzędnych wierzchołka 𝐷: 𝐷 = (−28, −17)
2 pkt – wyznaczenie równania prostej 𝐴𝐷 (lub 𝐷𝐶), np.


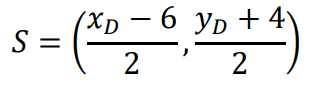
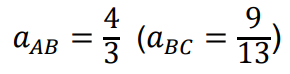
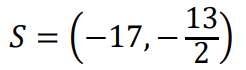
ALBO
zapisanie współrzędnych środka 𝑆 za pomocą współrzędnych wierzchołków 𝐵 i 𝐷:
1 pkt – obliczenie współczynnika kierunkowego prostej 𝐴𝐵 (lub 𝐵𝐶):
ALBO
obliczenie współrzędnych środka 𝑆 przekątnej 𝐴𝐶:
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.