Przekształcamy równanie prostej  𝐴𝐵  do postaci ogólnej:  3𝑥 + 𝑦 − 6 = 0. 

Obliczamy odległość wierzchołka  𝐶 = (3, 7)  od prostej  𝐴𝐵: 

Obliczona odległość  𝑑  jest wysokością trójkąta  𝐴𝐵𝐶  opuszczoną z wierzchołka  𝐶  na podstawę  𝐴𝐵. 

Obliczamy pole trójkąta  𝐴𝐵𝐶: 

𝑃 = ½ ⋅ 2√10 ⋅ √10 = 10

Wierzchołek  𝐴  leży na osi  𝑂𝑦, więc jego pierwsza współrzędna jest równa  0. 

Obliczamy drugą współrzędną wierzchołka  𝐴: 

𝑦 = −3𝑥 + 6  i   𝑥 = 0 𝑦 = −3 ⋅ 0 + 6 

czyli  𝐴 = (0, 6). 

Wierzchołek  𝐵  leży na osi  𝑂𝑥, więc jego druga współrzędna jest równa  0. 

Obliczamy pierwszą współrzędną wierzchołka  𝐵: 

𝑦 = −3𝑥 + 6  i   𝑦 = 0 

0 = −3𝑥 + 6 

𝑥 = 2 

Zatem  𝐵 = (2, 0). 

Pole trójkąta 𝐴𝐵𝐶 obliczymy korzystając z wzoru z Wybranych wzorów matematycznych: 

𝑃_{∆𝐴𝐵𝐶} = ½ |(𝑥𝐵 − 𝑥𝐴)(𝑦𝐶 − 𝑦𝐴) − (𝑦𝐵 − 𝑦𝐴)((𝑥𝐶 − 𝑥𝐴))| 

Obliczamy pole trójkąta  𝐴𝐵𝐶: 

𝑃_{∆𝐴𝐵𝐶} = ½ |(2 − 0)(7 − 6) − (0 − 6)(3 − 0)| =

= ½ |2 − (−18)| = 10. 

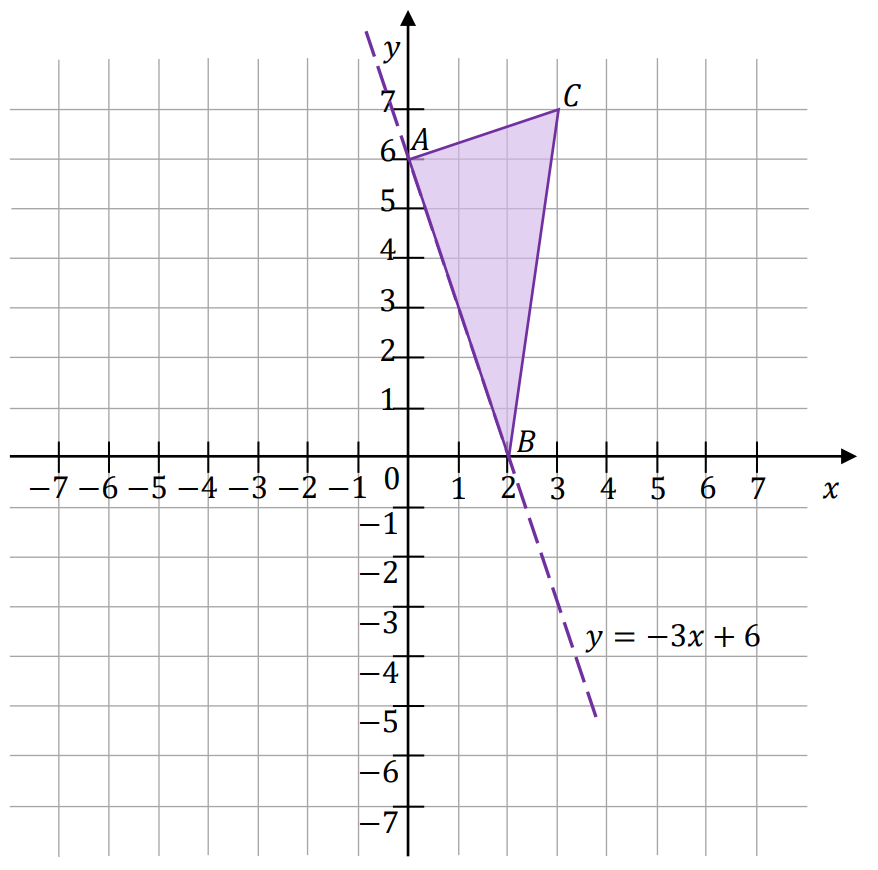
Rysunek ilustracyjny do zadania. 

2 pkt – obliczenie długości odcinka  𝐴𝐵:  |𝐴𝐵| = 2√10 

ALBO 

obliczenie odległości  𝑑  wierzchołka  𝐶  od prostej  𝐴𝐵i obliczenie współrzędnych wierzchołków  𝐴  i  𝐵:  𝑑 = √10, 𝐴 = (0, 6), 𝐵 = (2, 0) 

ALBO 

obliczenie współrzędnych wierzchołków  𝐴  i  𝐵:  𝐴 = (0, 6), 𝐵 = (2, 0) oraz zapisanie wzoru na pole  trójkąta z Wybranych wzorów matematycznych: 

𝑃_{∆𝐴𝐵𝐶} = ½ |(𝑥𝐵 − 𝑥𝐴)(𝑦𝐶 − 𝑦𝐴) − (𝑦𝐵 − 𝑦𝐴)((𝑥𝐶 − 𝑥𝐴))| 

1 pkt – obliczenie współrzędnych punktów  𝐴  i  𝐵:  𝐴 = (0 6), 𝐵 = (2, 0) 

ALBO 

obliczenie odległości  𝑑  punktu  𝐶  od prostej  𝐴𝐵:  𝑑 = √10. 

0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.