Odpowiedź:
Przykładowe pełne rozwiązania 

Sposób I 

Niech  𝑥𝑆  będzie pierwszą współrzędną środka  𝑆  okręgu  𝒪. 
Ponieważ  𝑆  leży na prostej  𝑘, więc  𝑆 = (𝑥𝑆 , 4𝑥𝑆 + 2). 
Punkty  𝐴  oraz  𝐵  leżą na okręgu, więc  |𝐴𝑆| = |𝐵𝑆|. 
Stąd otrzymujemy kolejno: 
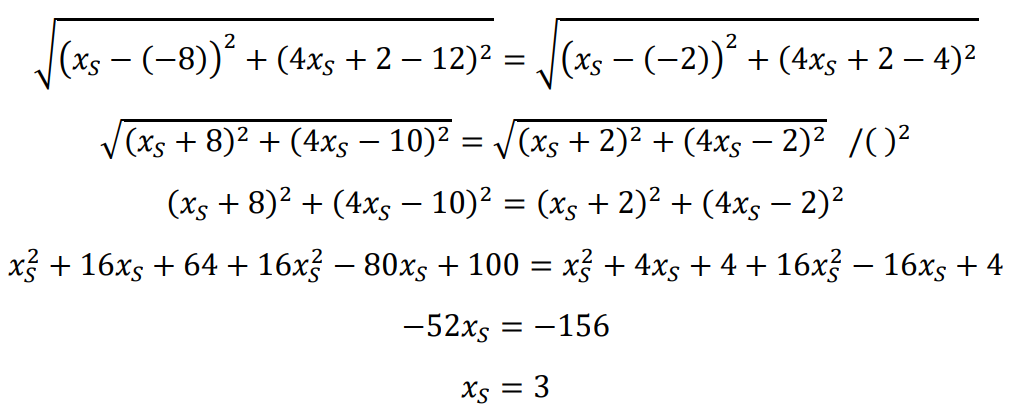
Zatem  4𝑥𝑆 + 2 = 4 ⋅ 3 + 2 = 14  i  𝑆 = (3, 14). 

Promień  𝑟  okręgu  𝒪  jest równy odległości punktu  𝐴  od środka  𝑆  okręgu, więc 

Sposób II 

Środek  𝑆  okręgu  𝒪  jest punktem przecięcia prostej  𝑘  z symetralną cięciwy  𝐴𝐵. 
W celu wyznaczenia równania symetralnej cięciwy  𝐴𝐵  należy: 
• obliczyć współrzędne środka  𝐷  cięciwy  𝐴𝐵 
• obliczyć współczynnik kierunkowy prostej zawierającej  𝐴𝐵 
• obliczyć współczynnik kierunkowy prostej, która jest prostopadła do  𝐴𝐵 
• wyznaczyć równanie prostej prostopadłej do  𝐴𝐵  i przechodzącej przez punkt  𝐷. 

Obliczamy współrzędne środka  𝐷  cięciwy  𝐴𝐵: 
Obliczamy współczynnik kierunkowy  𝑎1  prostej zawierającej cięciwę  𝐴𝐵: 

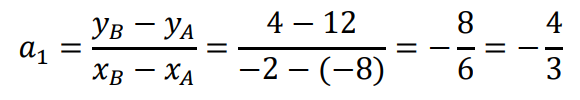
Obliczamy współczynnik kierunkowy  𝑎2  prostej prostopadłej do  𝐴𝐵: 

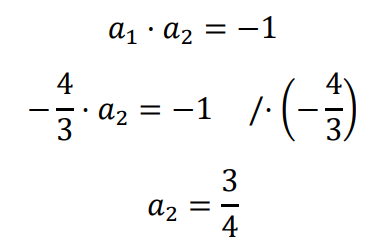
Wyznaczamy równanie symetralnej cięciwy  𝐴𝐵  (tj. prostej, która przechodzi przez środek cięciwy  𝐴𝐵  i jest prostopadła do  𝐴𝐵):

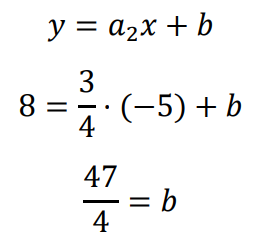
Zatem symetralna cięciwy  𝐴𝐵  ma równanie

Obliczamy współrzędne punktu przecięcia prostych o równaniach
i  𝑦 = 4𝑥 + 2:

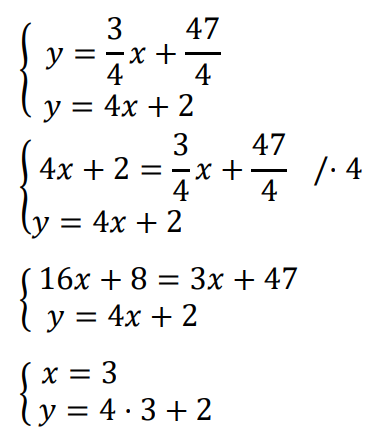
Środek  𝑆  okręgu  𝒪  ma współrzędne  𝑆 = (3, 14). 
Promień  𝑟  okręgu  𝒪  jest równy odległości punktu  𝐴  od środka  𝑆  okręgu, więc 
schemat punktacji
4 pkt – obliczenie promienia  𝑟  okręgu:  𝑟 = 5√5.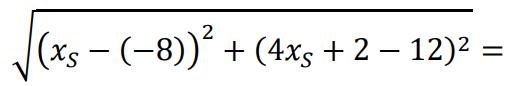 
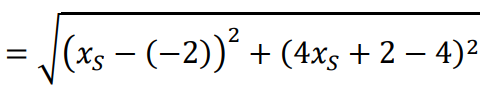
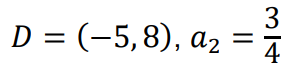
3 pkt – obliczenie współrzędnych środka  𝑆  okręgu:  𝑆 = (3, 14). 
2 pkt – zapisanie równania z jedną niewiadomą wynikającego z równości długości odcinków 𝐴𝑆  oraz  𝐵𝑆, np. 
ALBO 
obliczenie współrzędnych środka  𝐷  cięciwy  𝐴𝐵  oraz obliczenie współczynnika kierunkowego  𝑎2  prostej prostopadłej do  𝐴𝐵:
1 pkt – zapisanie współrzędnych środka  𝑆  okręgu w zależności od jednej zmiennej, np. 𝑆 = (𝑥𝑆 , 4𝑥𝑆 + 2) 
ALBO 
obliczenie współrzędnych środka  𝐷  cięciwy  𝐴𝐵:  𝐷 = (−5, 8), 
ALBO 
obliczenie współczynnika kierunkowego  𝑎1  prostej przechodzącej przez punkty  𝐴  i  𝐵: 𝑎1 = 4⁄3
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.