Odpowiedź:
Przykładowe pełne rozwiązania
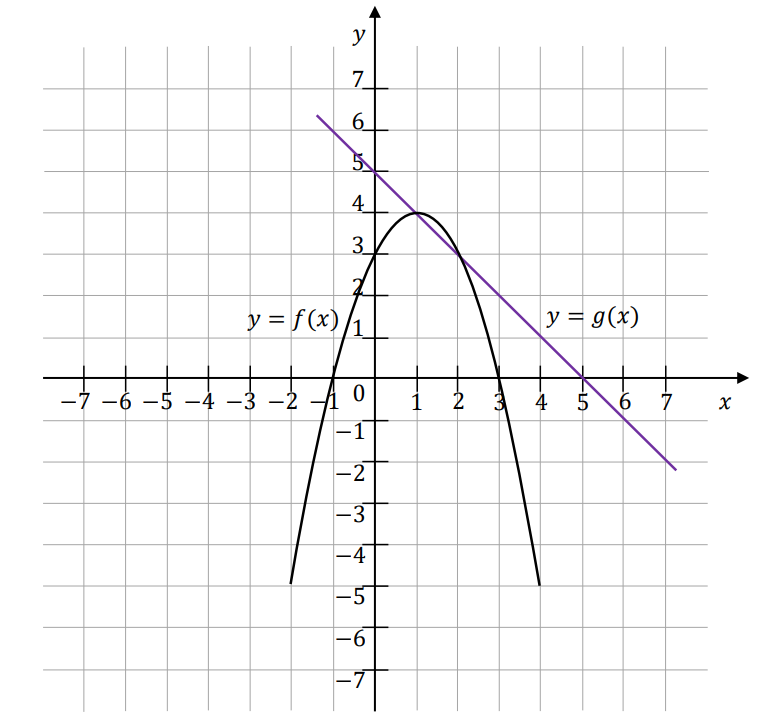
Rysunek ilustracyjny od zadania.
Sposób I
Rozwiązujemy układ równań:
Po podstawieniu do pierwszego z powyższych równań w miejsce 𝑦 wyrażenia −𝑥 + 5 otrzymujemy równanie z jedną niewiadomą:
−𝑥 + 5 = −𝑥² + 2𝑥 + 3
Przekształcamy to równanie równoważnie do postaci 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0 i rozwiązujemy:
𝑥² − 3𝑥 + 2 = 0
Δ = (−3)² − 4 ⋅ 1 ⋅ 2 = 9 − 8 = 1
𝑥1 = 1 lub 𝑥2 = 2
Obliczamy wartości drugich współrzędnych punktów wspólnych paraboli i prostej.
Dla 𝑥1 = 1 otrzymujemy 𝑦1 = −1 + 5 = 4.
Dla 𝑥2 = 2 otrzymujemy 𝑦2 = −2 + 5 = 3.
Wykresy funkcji przecinają się w punktach (1, 4) oraz (2, 3).
Sposób II
Przekształcamy wzór funkcji kwadratowej 𝑓(𝑥) = −𝑥² + 2𝑥 + 3 do postaci kanonicznej:
𝑓(𝑥) = −𝑥² + 2𝑥 + 3 = −𝑥² + 2𝑥 − 1 + 4 = −(𝑥² − 2𝑥 + 1) + 4 = −(𝑥 − 1)² + 4
Odczytujemy współrzędne wierzchołka 𝑊 paraboli, która jest wykresem funkcji 𝑓: 𝑊 = (1, 4). Rysujemy wykres funkcji 𝑓.
Ponieważ współczynnik przy 𝑥² we wzorze funkcji 𝑓 jest ujemny (𝑎 < 0), więc parabola ma ramiona skierowane ku dołowi.
Rysujemy prostą, która jest wykresem funkcji 𝑔 oraz parabolę, która jest wykresem funkcji 𝑓.
Na podstawie sporządzonych wykresów funkcji odczytujemy współrzędne punktów przecięcia: (1, 4) oraz (2, 3).
Sprawdzamy rachunkowo, czy punkty o odczytanych współrzędnych należą do wykresów obu funkcji:
𝑓(1) = −(1 − 1)² + 4 = 4
𝑔(1) = −1 + 5 = 4
Punkt (1, 4) należy do wykresów funkcji 𝑓 i 𝑔.
𝑓(2) = −(2 − 1)² + 4 = 3
𝑔(1) = −2 + 5 = 3
Punkt (2, 3) należy do wykresów funkcji 𝑓 i 𝑔.
Wykresy funkcji przecinają się w punktach (1, 4) oraz (2, 3).
schemat punktacji
3 pkt – obliczenie współrzędnych punktów przecięcia wykresów funkcji 𝑓 oraz 𝑔: (1, 4) oraz (2, 3)
ALBO
narysowanie wykresów funkcji 𝑓 oraz 𝑔, odczytanie i zapisanie współrzędnych punktów przecięcia wykresów tych funkcji oraz sprawdzenie rachunkiem, że punkty o odczytanych współrzędnych należą jednocześnie do wykresów każdej z funkcji.
2 pkt – rozwiązanie równania kwadratowego −𝑥 + 5 = −𝑥² + 2𝑥 + 3: 𝑥1 = 1 oraz 𝑥2 = 2
ALBO
narysowanie wykresów funkcji 𝑓 oraz 𝑔 oraz odczytanie i zapisanie współrzędnych punktów przecięcia wykresów tych funkcji.
1 pkt – zapisanie równania kwadratowego −𝑥 + 5 = −𝑥² + 2𝑥 + 3
ALBO
narysowanie wykresu funkcji kwadratowej 𝑓 lub wykresu funkcji liniowej 𝑔.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.