Pole ostrosłupa  𝐴𝐵𝐷𝐸  jest równe sumie pól trzech przystających trójkątów równoramiennych prostokątnych (𝐴𝐵𝐷,  𝐴𝐵𝐸  i  𝐴𝐷𝐸)  oraz trójkąta równobocznego  𝐵𝐷𝐸.

Trójkąt prostokątny stanowi połowę ściany sześcianu , zatem jego pole to  ½ 𝑎². Bok trójkąta równobocznego jest przekątną ściany bocznej sześcianu, zatem ma długość  𝑎√2. Jego pole to 

Obliczamy pole powierzchni ostrosłupa  𝐴𝐵𝐷𝐸, dodając pola trzech trójkątów prostokątnych i pole trójkąta równobocznego: 

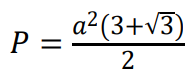
1 pkt – zapisanie, że pole powierzchni ostrosłupa  𝐴𝐵𝐷𝐸  jest równe sumie pól trzech trójkątów prostokątnych oraz pola trójkąta równobocznego. 

0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.