Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.

Rozwiązaniami równania postaci 𝑉(𝑥) ⁄𝑊(𝑥) = 0 są takie liczby 𝑥𝑖 , dla których:

𝑉(𝑥𝑖 ) = 0 oraz 𝑊(𝑥𝑖 ) ≠ 0

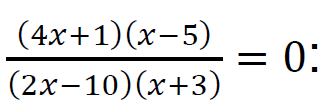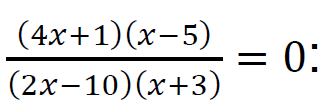Mianownik ułamka 7.1.png  musi być różny od zera, zatem:

(2𝑥 − 10)(𝑥 + 3) ≠ 0

Iloczyn jest różny od zera, gdy każdy z czynników iloczynu jest różnym od zera:

2𝑥 − 10 ≠ 0 oraz 𝑥 + 3 ≠ 0

𝑥 ≠ 5 oraz 𝑥 ≠ −3

Gdy mianownik ułamka jest różny od zera, to ułamek jest wtedy równy zero, gdy licznik jest równy zero, zatem:

(4𝑥 + 1)(𝑥 − 5) = 0

Iloczyn jest równy zero, gdy co najmniej jeden z jego czynników jest równy zero:

4𝑥 + 1 = 0 lub 𝑥 − 5 = 0

𝑥 =  − 1⁄4   lub 𝑥 = 5

Ponieważ 𝑥 ≠ 5, to rozwiązaniem równania jest liczba 𝑥 = −1⁄4.

Sposób 2.

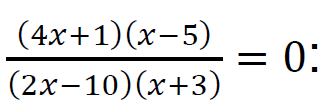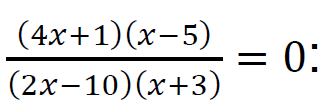Wyrażenie po lewej stronie równania  7.1.png  ma sens liczbowy, gdy:

(2𝑥 − 10)(𝑥 + 3) ≠ 0

𝑥 ≠ 5 oraz 𝑥 ≠ −3

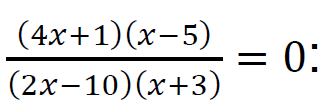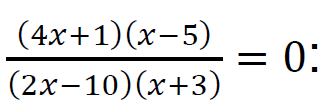Zatem równanie 7.1.png  jest określone dla 𝑥 ∈ ℝ\{5, −3}. Przekształcimy
równoważnie równanie:


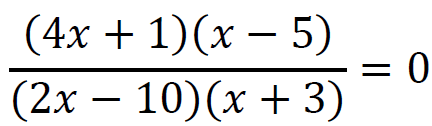
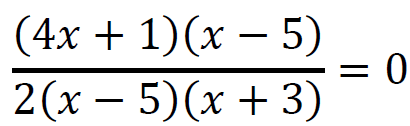
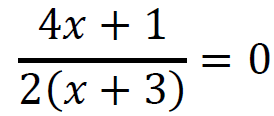
Gdy mianownik ułamka jest różny od zera, to ułamek jest wtedy równy zero, gdy licznik jest równy zero, zatem:

4𝑥 + 1 = 0

𝑥 = −1⁄4




schemat punktacji
2 pkt – poprawna metoda rozwiązania równania podanego w treści zadania (rozwiązanie
równania (4𝑥 + 1)(𝑥 − 5) = 0 lub równania 4𝑥 + 1 = 0 oraz wyznaczenie dziedziny
równania) i podanie wyniku: 𝑥 = − 1⁄4 
1 pkt – poprawne rozwiązanie równania (4𝑥 + 1)(𝑥 − 5) = 0 : 𝑥 = − 1⁄4   lub 𝑥 = 5
LUB
– poprawne wyznaczenie dziedziny równania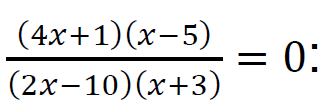 
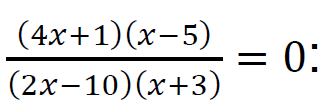
𝑥 ≠ 5 oraz 𝑥 ≠ −3.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.