Odpowiedź:
Przykładowe pełne rozwiązania
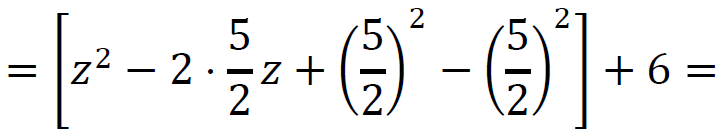
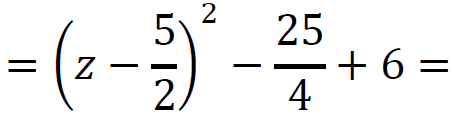
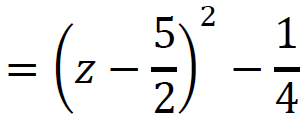

Zauważmy, że równanie w tym zadaniu jest przykładem równania dwukwadratowego. Dlatego w równaniu (𝑥 − 1)4 − 5(𝑥 − 1)2 + 6 = 0 podstawiamy 𝑧 = (𝑥 − 1)2, gdzie 𝑧 ≥ 0, po czym otrzymujemy równanie kwadratowe z niewiadomą 𝑧:
𝑧2 − 5𝑧 + 6 = 0 𝑧 = (𝑥 − 1)2 gdzie 𝑧 ≥ 0
Sposób 1. rozwiązania równania 𝑧2 − 5𝑧 + 6 = 0
Rozwiążemy równanie kwadratowe wykorzystując metodę dopełnienia wyrażenia do pełnego kwadratu. Przekształcimy równoważnie trójmian kwadratowy po lewej stronie równania:
(𝑧2 − 5𝑧) + 6 =
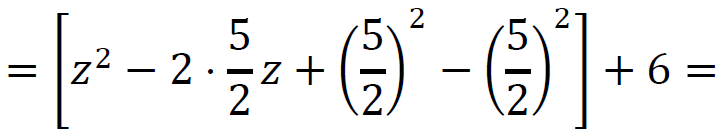
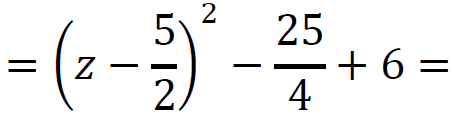
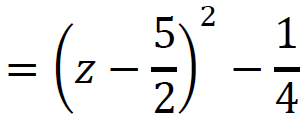
Rozwiążemy równanie po przekształceniu równoważnym:
(z − 5⁄2 )2 − 1⁄4 = 0 zatem (z − 5⁄2 )2 = 1⁄4
| z − 5⁄2 | = 1⁄2
z − 5⁄2 = 1⁄2 lub z − 5⁄2 = − 1⁄2
𝑧 = 3 lub 𝑧 = 2
Sposób 2. rozwiązania równania 𝑧2 − 5𝑧 + 6 = 0
Obliczymy tzw. wyróżnik równania kwadratowego (zobacz w Wybranych wzorach
matematycznych):
Δ𝑧 = 𝑏2 − 4𝑎𝑐 = (−5)2 − 4 ⋅ 1 ⋅ 6 = 1.
Ponieważ Δ𝑧 > 0 to możemy zastosować gotowe wzory (podane w Wybranych wzorach
matematycznych) na rozwiązania równania kwadratowego:

Rozwiązania równania kwadratowego:
𝑧1 = 2 lub 𝑧2 = 3
Powracamy do podstawienia 𝑧 = (𝑥 − 1)2 i wyznaczamy rozwiązania równania podanego w zadaniu:
(𝑥 − 1)2 = 2 lub (𝑥 − 1)2 = 3
|𝑥 − 1| = √2 lub |𝑥 − 1| = √3
Stąd:
𝑥11 = √2 + 1 , 𝑥12 = − √2 + 1 , 𝑥21 = √3 +1 +, 𝑥22 = − √3 + 1 .
schemat punktacji
3 pkt – poprawna metoda rozwiązania równania oraz podanie prawidłowych rozwiązań:
𝑥11 = 1 + √2 , 𝑥12 = 1 − √2 , 𝑥21 = 1 + √3 , 𝑥22 = 1 − √3 .
2 pkt – rozwiązanie równania 𝑧2 − 5𝑧 + 6 = 0: 𝑧1 = 2, 𝑧2 = 3 oraz zapisanie równań równoważnych: 2 = (𝑥 − 1)2, 3 = (𝑥 − 1)2
LUB
– prawidłowe obliczenie jednego z pierwiastków równania 𝑧2 − 5𝑧 + 6 = 0: 𝑧1 = 2 (drugi pierwiastek obliczony błędnie lub wcale) albo 𝑧2 = 3 (drugi pierwiastek obliczony
błędnie lub wcale) oraz konsekwentne – z tym prawidłowo wyznaczonym pierwiastkiem
– rozwiązanie równania podanego w zadaniu i zapisanie:
𝑥1 = 1 + √2 , 𝑥2 = 1 − √2 albo 𝑥1 = 1 + √3 , 𝑥2 = 1 − √3 .
1 pkt – wykonanie odpowiedniego podstawienia i przekształcenie do równania postaci
równoważnej równaniu 𝑧2 − 5𝑧 + 6 = 0, gdzie 𝑧 ≥ 0.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.