Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Wykorzystamy informację podaną w zadaniu. Zapiszemy wielomian 𝑊(𝑥) w postaci iloczynu
dwumianu 𝑥 + 2 i wielomianu 𝑄(𝑥):
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = (𝑥 + 2)𝑄(𝑥)
Wielomian 𝑄(𝑥) jest trójmianem kwadratowym, zatem powyższą równość zapiszemy w postaci:
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = (𝑥 + 2)(𝑎𝑥2 + 𝑏𝑥 + 𝑐)
dla pewnych liczb rzeczywistych a, b, c. Prawą stronę przekształcimy do postaci sumy
algebraicznej wyrażeń z potęgą zmiennej 𝑥. Następnie, aby obliczyć współczynniki a, b, c, m porównamy wyrażenia z odpowiednimi potęgami zmiennej 𝑥 po prawej i lewej stronie równości:
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = 𝑎𝑥3 + 𝑏𝑥2 + 𝑐𝑥 + 2𝑎𝑥2 + 2𝑏𝑥 + 2𝑐
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = 𝑎𝑥3 + (𝑏 + 2𝑎)𝑥2 + (𝑐 + 2𝑏)𝑥 + 2𝑐
Współczynniki przy kolejnych potęgach 𝑥 muszą być równe, zatem:
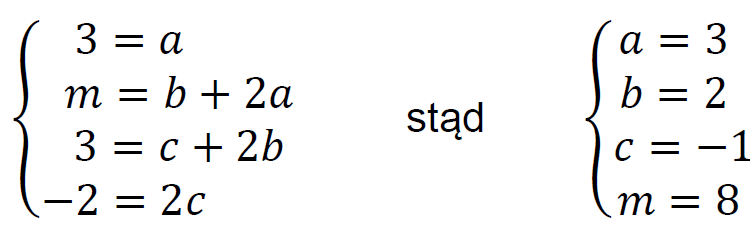
Wielomian 𝑄(𝑥) ma postać 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1. Pierwiastki wielomianu 𝑊(𝑥) obliczymy z jego postaci iloczynowej:
𝑊(𝑥) = (𝑥 + 2)(3𝑥2 + 2𝑥 − 1) = 0
stąd
𝑥 + 2 = 0 lub 3𝑥2 + 2𝑥 − 1 = 0
𝑥 = −2 lub 𝑥 = −1 lub 𝑥 = 1⁄3
Sposób 2.
Wyznaczymy jeden z pierwiastków 𝑊(𝑥). Wykorzystamy informację o rozkładzie wielomianu 𝑊(𝑥) na czynniki:
𝑊(𝑥) = (𝑥 + 2)𝑄(𝑥) = 0
stąd 𝑥 + 2 = 0 czyli 𝑥 = −2
Obliczymy 𝑚. Ponieważ 𝑊(−2) = 0, to:
𝑊(−2) = 3 ⋅ (−2)3 + 𝑚(−2)2 + 3 ⋅ (−2) − 2 = 0
−24 + 4𝑚 − 8 = 0
𝑚 = 8
Zatem:
𝑊(𝑥) = 𝑥3 + 8𝑥2 + 3𝑥 − 2
Wyznaczymy 𝑄(𝑥) – zastosujemy algorytm dzielenia wielomianów:
𝑊(𝑥) = (𝑥 + 2)𝑄(𝑥) stąd 𝑊(𝑥): (𝑥 + 2) = 𝑄(𝑥)
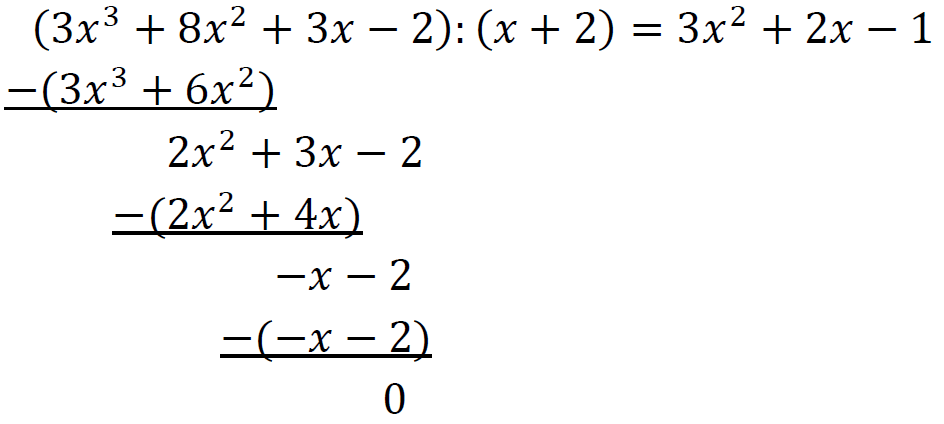
Zatem:
𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1
Pozostałe pierwiastki wielomianu 𝑊(𝑥) = 3𝑥3 + 8𝑥2 + 3𝑥 − 2 obliczymy korzystając z jego postaci iloczynowej, gdy znamy 𝑄(𝑥):
𝑊(𝑥) = (𝑥 + 2)(3𝑥2 + 2𝑥 − 1) = 0
stąd:
𝑥 + 2 = 0 lub 3𝑥2 + 2𝑥 − 1 = 0
𝑥 = −2 lub 𝑥 = −1 lub 𝑥 = 1⁄3
Sposób 3.
Wykorzystamy informację podaną w zadaniu o rozkładzie 𝑊(𝑥) na czynniki:
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = (𝑥 + 2)𝑄(𝑥)
Z powyższego zapisu iloczynowego wynika, że: 𝑄(𝑥) = (3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2): (𝑥 + 2).
Zastosujemy algorytm dzielenia wielomianów:
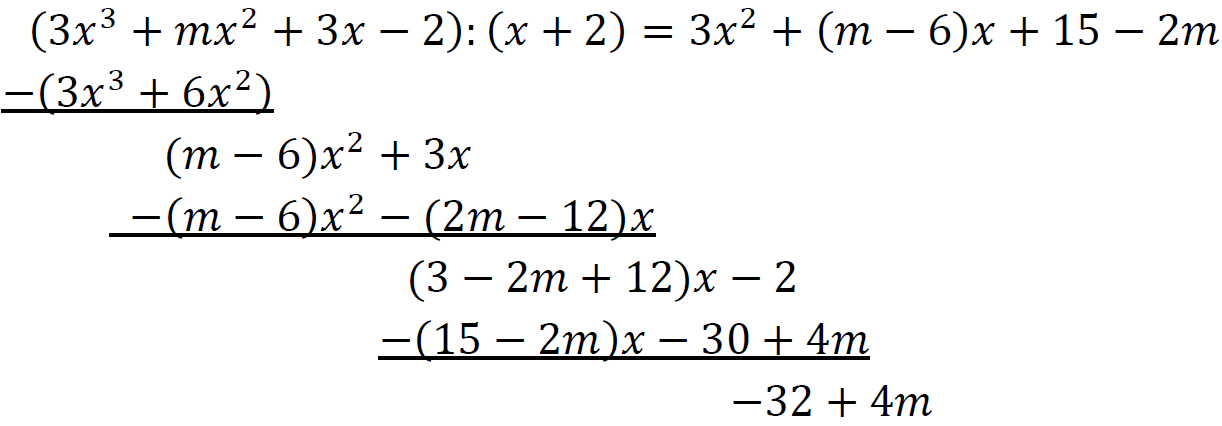
Zatem:
𝑄(𝑥) = 3𝑥2 + (𝑚 − 6)𝑥 + 15 − 2𝑚
a reszta z dzielenia 𝑊(𝑥) przez (𝑥 + 2) jest dana wyrażeniem:
𝑅(𝑥) = −32 + 4𝑚
Na podstawie zapisu iloczynowego 𝑊(𝑥) = (𝑥 + 2)𝑄(𝑥) wnioskujemy, że reszta z dzielenia 𝑊(𝑥): (𝑥 + 2) jest równa zero:
𝑅(𝑥) = 0 zatem − 32 + 4𝑚 = 0 więc 𝑚 = 8
Stąd:
𝑄(𝑥) = 3𝑥2 + (8 − 6)𝑥 + 15 − 2𝑚 = 3𝑥2 + 2𝑥 − 1
Pozostałe pierwiastki wielomianu 𝑊(𝑥) = (𝑥 + 2)(3𝑥2 + 2𝑥 − 1) obliczymy rozwiązując
równanie 𝑄(𝑥) = 0:
3𝑥2 + 2𝑥 − 1 = 0
𝑥1 = 1⁄3 lub 𝑥2 = −1
schemat punktacji
Zasady oceniania
dla rozwiązania sposobem 1.
3 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), obliczenie pierwiastków wielomianu 𝑊(𝑥) oraz podanie wyników: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1, 𝑥1 = −2, 𝑥2 = −1, 𝑥3 = 1⁄3 .
2 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥) oraz prawidłowa postać tego
wielomianu: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1
LUB
– poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), błędy w obliczeniach
współczynników a, b, c oraz poprawna metoda wyznaczenia pierwiastków wielomianu
𝑊(𝑥), tzn.: zapisanie 𝑥 + 2 = 0, 𝑄(𝑥) = 0 oraz rozwiązanie obu równań.
1 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), tzn.: zapisanie równania
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = (𝑥 + 2)(𝑎𝑥2 + 𝑏𝑥 + 𝑐) oraz postępowanie prowadzące do
wyznaczenia a, b, c: przekształcenie prawej strony do sumy algebraicznej
i porównywanie współczynników przy tych samych potęgach 𝑥 po lewej i prawej stronie równania.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
Zasady oceniania
dla rozwiązania sposobem 2.
3 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), obliczenie pierwiastków wielomianu
𝑊(𝑥) oraz podanie wyników: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1, 𝑥1 = −2, 𝑥2 = −1, 𝑥3 = 1⁄3 .
2 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), tzn. zastosowanie algorytmu
dzielenia wielomianu 𝑊(𝑥) przez dwumian 𝑥 + 2 albo zapisanie
3𝑥3 + 8𝑥2 + 3𝑥 − 2 = (𝑥 + 2)(𝑎𝑥2 + 𝑏𝑥 + 𝑐) oraz postępowanie prowadzące do wyznaczenia a, b, c, oraz poprawna postać tego wielomianu: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1
LUB
poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), błędy w obliczeniach oraz
poprawna metoda obliczenia pierwiastków wielomianu 𝑊(𝑥), tzn. zapisanie 𝑥 + 2 = 0, 𝑄(𝑥) = 0 oraz rozwiązanie obu równań.
1 pkt – zapisanie, że 𝑊(−2) = 0, oraz poprawne obliczenie współczynnika 𝑚 = 8
LUB
– zapisanie, że 𝑊(−2) = 0, błędy w obliczeniach przy wyznaczeniu 𝑚 oraz
postępowanie prowadzące do wyznaczenia wielomianu 𝑄(𝑥), tzn. zastosowanie algorytmu dzielenia wielomianu 𝑊(𝑥) przez dwumian 𝑥 + 2 albo zapisanie
3𝑥3 + 𝑚𝑥2 + 3𝑥 − 2 = (𝑥 + 2)(𝑎𝑥2 + 𝑏𝑥 + 𝑐), oraz postępowanie prowadzące do
wyznaczenia a, b, c.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
Zasady oceniania
dla rozwiązania sposobem 3.
3 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), obliczenie pierwiastków wielomianu 𝑊(𝑥) oraz podanie wyników: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1, 𝑥1 = −2, 𝑥2 = −1, 𝑥3 = 1⁄3 .
2 pkt – poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), tzn. zastosowanie algorytmu
dzielenia wielomianu 𝑊(𝑥) przez dwumian 𝑥 + 2 oraz prawidłowa postać tego
wielomianu: 𝑄(𝑥) = 3𝑥2 + 2𝑥 − 1
LUB
– poprawna metoda wyznaczenia wielomianu 𝑄(𝑥), błędy w obliczeniach oraz
poprawna metoda obliczenia pierwiastków wielomianu 𝑊(𝑥), tzn. zapisanie
𝑥 + 2 = 0, 𝑄(𝑥) = 0 oraz rozwiązanie obu równań.
1 pkt – zastosowanie algorytmu dzielenia wielomianu 𝑊(𝑥) przez dwumian 𝑥 + 2 oraz
poprawne obliczenie współczynnika 𝑚 = 8.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.