Odpowiedź:
Przykładowe pełne rozwiązanie
Komentarz (krok 1.)
Do obliczenia wartości siły wykorzystamy II zasadę dynamiki: iloraz zmiany wektora pędu ciała i czasu, w którym ta zmiana nastąpiła, jest równy sile działającej na ciało w tym czasie:
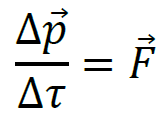
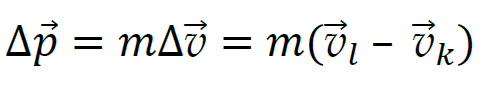
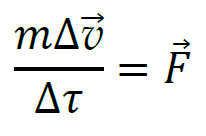

Komentarz (krok 2.)
Wyznaczymy zmianę 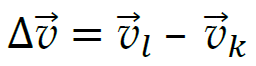 wektora prędkości, a następnie obliczymy jej wartość. Na podstawie położeń ciała określimy składowe
wektora prędkości, a następnie obliczymy jej wartość. Na podstawie położeń ciała określimy składowe 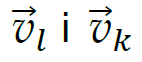 w kierunku 𝑥 oraz 𝑦. Pierwsza liczba w nawiasie kwadratowym to współrzędna składowej 𝑥, a druga – współrzędna składowej 𝑦:
w kierunku 𝑥 oraz 𝑦. Pierwsza liczba w nawiasie kwadratowym to współrzędna składowej 𝑥, a druga – współrzędna składowej 𝑦:
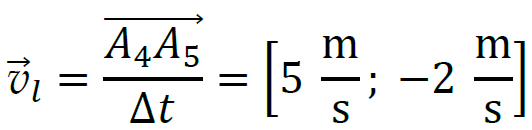
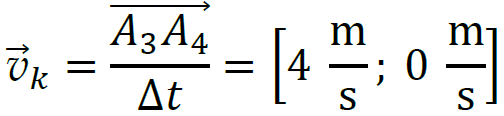
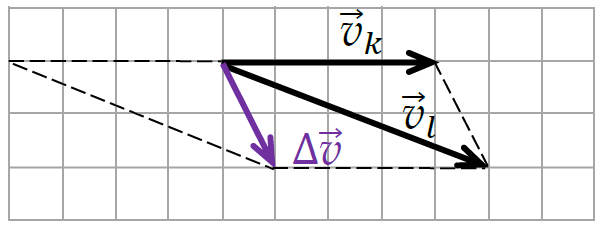
Odejmowanie wektorów prędkości wykonamy np. graficznie (rysunek poniżej). Niech długość boku kratki odpowiada jednostce prędkości wyrażonej w m/s. Po odjęciu wektorów obliczymy wartość różnicy prędkości:
Różnica prędkości ma współrzędne:
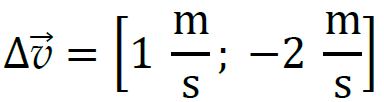
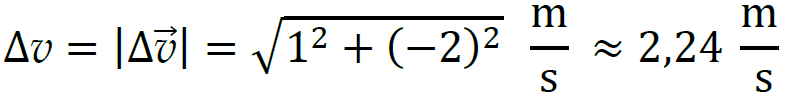
Komentarz (krok 3.)
Obliczymy wartość siły (dane i wynik w kroku 2. podstawimy do wzoru w kroku 1.).
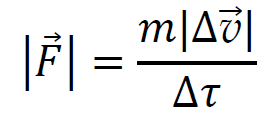 →
→ 
schemat punktacji
3 pkt – poprawna metoda obliczenia siły oraz prawidłowy wynik liczbowy z jednostką (np. jak w krokach 1., 2. i 3.).
2 pkt – wykorzystanie drugiej zasady dynamiki wyrażonej w postaci związku między zmianą pędu i siłą oraz obliczenie wartości zmiany prędkości (np. jak w krokach 1. i 2.).
1 pkt – wykorzystanie drugiej zasady dynamiki wyrażonej w postaci związku między zmianą wektora pędu, czasem, w którym ta zmiana nastąpiła, a siłą – łącznie z wyrażeniem zmiany pędu jako 𝑚Δ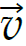 (np. jak w kroku 1.)
(np. jak w kroku 1.)
LUB
– wykorzystanie drugiej zasady dynamiki wyrażonej w postaci związku między masą, siłą a przyśpieszeniem – łącznie z wyrażeniem wektora przyśpieszenia jako zmiany
wektora prędkości w czasie
LUB
– obliczenie wartości różnicy wektorów prędkości lub obliczenie wartości różnicy
wektorów pędu (np. jak w kroku 2.).
Uwaga! Obliczenie różnicy wartości wektorów prędkości lub pędów jest błędem rzeczowym.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.