Odpowiedź:
Przykładowe pełne rozwiązanie
Komentarz (krok 1.)
Wykorzystamy zasadę zachowania pędu całkowitego układu: wektorowa suma pędów ciał A i B przed zderzeniem jest równa wektorowej sumie pędów ciał A i B po zderzeniu:
To oznacza, że pęd całkowity jest zachowany w kierunku 𝑥 oraz w kierunku 𝑦, z czego dalej skorzystamy.
Komentarz (krok 2.)
Ustalimy współrzędne prędkości ciał A i B wyrażone w jednostkach umownych (ju). Za
jednostkę długości przyjmiemy bok najmniejszej kratki na diagramie, a za jednostkę czasu – czas upływający między kolejnymi zdjęciami. Skorzystamy z wygodnego sposobu zapisu składowych wektora we współrzędnych (pierwsza w nawiasie kwadratowym to współrzędna składowej 𝑥, druga – współrzędna składowej 𝑦):
= [v𝐴𝑥 𝑝𝑟𝑧𝑒𝑑; v𝐴𝑦 𝑝𝑟𝑧𝑒𝑑] = [18,5 ju; 0 ju]
= [v𝐴𝑥 𝑝𝑜; v𝐴𝑦 𝑝𝑜] = [8,5 ju; − 7,5 ju]
= [v𝐵𝑥 𝑝𝑜; v𝐵𝑦 𝑝𝑜 ] = [8 ju; 6 ju]Komentarz (krok 3.)
Podstawimy współrzędne prędkości do zasady zachowania pędu:
𝑚𝐴 ∙ [18,5 ju; 0 ju] = 𝑚𝐴 ∙ [8,5 ju; − 7,5 ju] + 𝑚𝐵 ∙ [8 ju; 6 ju]
Przyrównamy współrzędne 𝑥 i 𝑦 pędu układu przed zderzeniem i po zderzeniu:
→ 
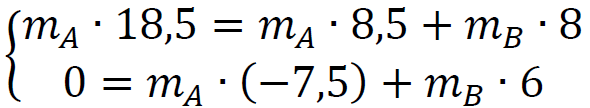
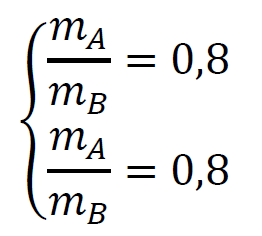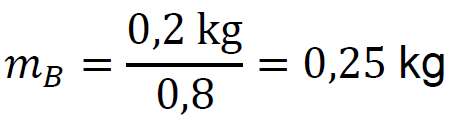
schemat punktacji
3 pkt – poprawna metoda obliczenia masy ciała B i prawidłowy wynik liczbowy z jednostką (np. jak w krokach 1–3.).
2 pkt – poprawne zapisanie zasady zachowania pędu całkowitego układu, łącznie z prawidłowym wyrażeniem współrzędnych prędkości ciał A i B przed zderzeniem i po zderzeniu w umownych jednostkach (np. jak w kroku 1. i kroku 2.).
1 pkt – przyrównanie pędu ciała A przed zderzeniem do wektorowej sumy pędów ciał A i B po zderzeniu (np. jak w kroku 1.).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.