Odpowiedź:
Przykładowe pełne rozwiązanie
Komentarz (krok 1.)
Powołamy się na własność zderzenia sprężystego.
W zderzeniu sprężystym całkowita energia mechaniczna układu po zderzeniu byłaby równa całkowitej energii mechanicznej układu przed zderzeniem. W zderzeniu, które nie jest sprężyste, całkowita energia mechaniczna układu po zderzeniu będzie mniejsza od energii przed zderzeniem. Ponieważ ruch odbywa się w płaszczyźnie poziomej, a ciała poza zderzeniem nie oddziałują, to całkowita energia mechaniczna układu jest energią kinetyczną układu.
Komentarz (krok 2.)
Zapiszemy wyrażenia na energię mechaniczną układu:
𝐸𝑝𝑟𝑧𝑒𝑑 = 1⁄2𝑚𝐴v2𝐴𝑝𝑟𝑧𝑒𝑑 𝐸𝑝𝑜 = 1⁄2𝑚𝐴v2𝐴 𝑝𝑜 + 1⁄2𝑚𝐵 v2𝐵 𝑝𝑜
Do obliczenia kwadratów wartości prędkości musimy ustalić współrzędne prędkości wyrażone w jednostkach umownych ju. Za jednostkę długości przyjmiemy bok kratki na diagramie, a za jednostkę czasu – czas upływający między kolejnymi zdjęciami:
= [v𝐴𝑥 𝑝𝑟𝑧𝑒𝑑; v𝐴𝑦 𝑝𝑟𝑧𝑒𝑑] = [18,5 ju; 0 ju]
= [v𝐴𝑥 𝑝𝑜; v𝐴𝑦 𝑝𝑜] = [8,5 ju; − 7,5 ju]
= [v𝐵𝑥 𝑝𝑜; v𝐵𝑦 𝑝𝑜 ] = [8 ju; 6 ju]Komentarz (krok 3.)
W celu zbadania, czy energia mechaniczna układu jest zachowana, obliczymy iloraz energii po zderzeniu i przed zderzeniem (tak uniezależnimy wynik od jednostek, ponadto gdyby zderzenie miało być sprężyste, ten iloraz byłby równy 1):
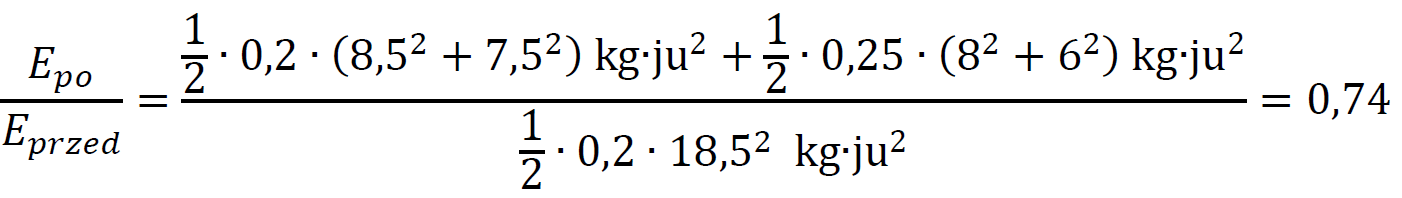
W wyniku zderzenia ciało straciło 26% energii mechanicznej. Taka rozbieżność nie może wynikać z niedokładności pomiarów z diagramu, zatem zderzenie nie było sprężyste.
schemat punktacji
3 pkt – poprawna metoda, prawidłowy rezultat obliczeń oraz ustalenie i zapisanie, że zderzenie nie było sprężyste (np. jak w krokach 1.–3.).
2 pkt – poprawne zapisanie i porównywanie wyrażeń opisujących całkowitą energię kinetyczną układu przed zderzeniem oraz całkowitą energię kinetyczną układu po zderzeniu, łącznie z prawidłową identyfikacją współrzędnych wszystkich prędkości (np. jak w kroku 1. i kroku 2.).
1 pkt – zastosowanie metody polegającej na sprawdzeniu, czy całkowita energia kinetyczna zostanie zachowana przy zderzeniu, czy też nie
LUB
– powołanie się (wystarczy opis słowny) na własność zderzenia sprężystego łącznie z identyfikacją energii mechanicznej układu jako energii kinetycznej układu (np. jak w kroku 1.).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.