Odpowiedź:
Przykładowe pełne rozwiązanie
Komentarz (krok 1.)
Na walec oraz ciężarki działają sznurki siłami o wartościach 𝐹1 i 𝐹2. Na rysunku poniżej
przedstawiono siły działające w układzie. Zgodnie z nim zapiszemy równania ruchu ciężarków oraz walca. Uwzględnimy fakt, że ciężarek 𝑚2 opada oraz fakt, że oba ciężarki mają przeciwne przyśpieszenia:


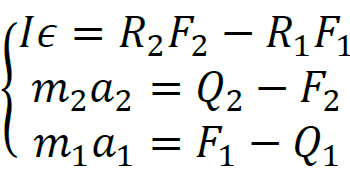
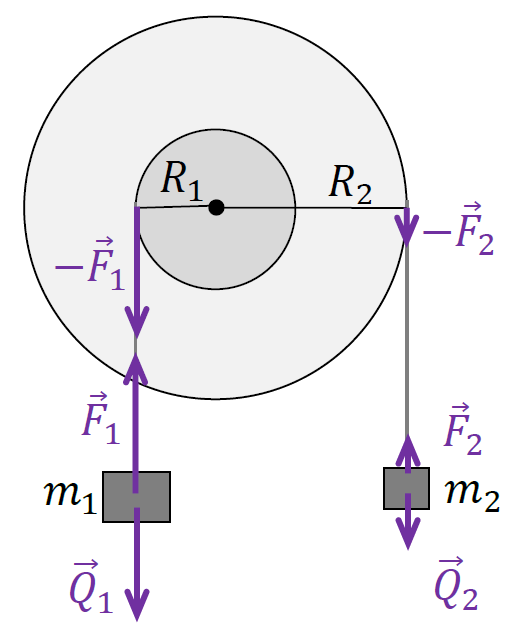
Komentarz (krok 2.)
Uwzględnimy związki między przyśpieszeniem kątowym bryły połączonych walców
a przyśpieszeniami liniowymi ciężarków. Ponadto zapiszemy moment bezwładności 𝐼
kołowrotu jako sumę momentów bezwładności obu walców:

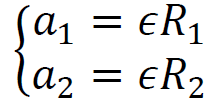
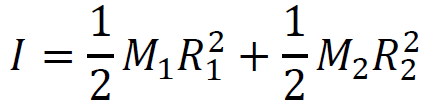   →          𝐼  ≈ 0,0614 kg∙m2

Komentarz (krok 3.)
Z powyższych równań wyznaczymy przyśpieszenie 𝜖 kątowe bryły obrotowej:

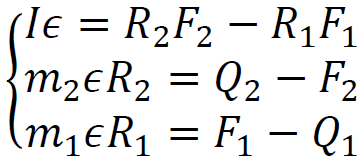4.5.png  →      → 

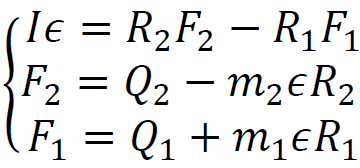𝐼𝜖 = 𝑅2(𝑄2 − 𝑚2𝜖𝑅2) − 𝑅1(𝑄1 + 𝑚1𝜖𝑅1)

𝐼𝜖 = 𝑅2𝑚2𝑔 − 𝑚2𝜖𝑅22 − 𝑅1𝑚1𝑔 − 𝑚1𝜖𝑅21


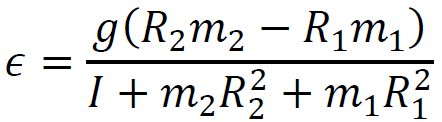
Komentarz (krok 4.)
Obliczamy 𝑎1:

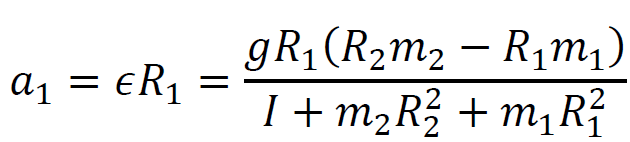
𝑎1 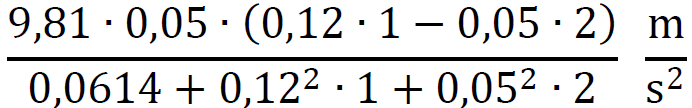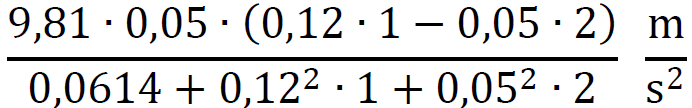≈  ≈ 0,12 m⁄s2
schemat punktacji
4 pkt – poprawna metoda obliczenia przyśpieszenia 𝑎1 oraz prawidłowy wynik liczbowy z jednostką (np. jak w krokach 1.–4.).
3 pkt – poprawne rozwiązanie układu równań, z którego można wyznaczyć przyśpieszenie kątowe na podstawie danych w zadaniu ( np. jak w kroku 3.).
2 pkt – poprawne zapisanie trzech równań ruchu, łącznie z uwzględnieniem związków między przyśpieszeniami liniowymi a przyśpieszeniem kątowym, oraz zapisanie wzoru na moment bezwładności bryły (np. jak w krokach 1. i 2.).
1 pkt – poprawne zapisanie trzech równań ruchu wyrażających drugą zasadę dynamiki: równania ruchu obrotowego bryły, równania ruchu postępowego ciężarka o masie 𝑚1 oraz równania ruchu postępowego ciężarka o masie 𝑚1 – łącznie z odróżnieniem przyśpieszeń liniowych obu ciężarków (np. jak w kroku 1.).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.