Odpowiedź:
Przykładowe pełne rozwiązania
Ruch po orbicie eliptycznej prawidłowo zilustrowano rysunkiem nr 1.
Uzasadnienie:
Sposób 1. (Zastosowanie drugiej zasady dynamiki)
Komentarz
Porównamy zwroty wektorów: 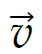 – prędkości ciała i
– prędkości ciała i 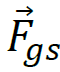 – stycznej składowej siły grawitacji, gdy ciało oddala się od masy 𝑀 (zobacz rysunek). Składowa grawitacji prostopadła do składowe stycznej, nie wpływa na przyśpieszenie wzdłuż toru.
– stycznej składowej siły grawitacji, gdy ciało oddala się od masy 𝑀 (zobacz rysunek). Składowa grawitacji prostopadła do składowe stycznej, nie wpływa na przyśpieszenie wzdłuż toru.
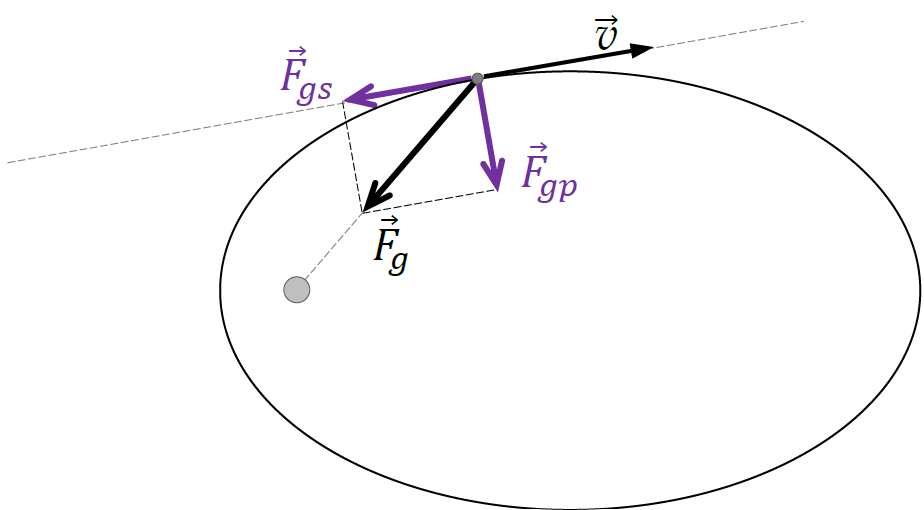
Zauważmy, że poza punktami na orbicie leżącymi najbliżej i najdalej od gwiazdy (perycentrum i apocentrum) siła grawitacji 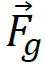 działająca na ciało o masie 𝑚 ma składową
działająca na ciało o masie 𝑚 ma składową 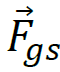 styczną do elipsy oraz składową
styczną do elipsy oraz składową 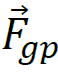 prostopadłą do stycznej. Gdy ciało oddala się od masy 𝑀, to
prostopadłą do stycznej. Gdy ciało oddala się od masy 𝑀, to 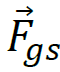 ma przeciwny zwrot do wektora
ma przeciwny zwrot do wektora 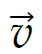 prędkości ciała poruszającego się po orbicie eliptycznej.
prędkości ciała poruszającego się po orbicie eliptycznej.
Wykorzystamy drugą zasadę dynamiki.
Zgodnie z drugą zasadą dynamiki, w takiej sytuacji ciało ma przyśpieszenie (opóźnienie) w kierunku stycznym przeciwne do zwrotu prędkości. Zatem wartość prędkości od perycentrum do apocentrum maleje (położenia ciała na rysunku 1. są coraz gęściej).
Analogicznie opiszemy sytuację, gdy ciało zbliża się do masy 𝑀.
Gdy ciało porusza się od apocentrum do perycentrum (czyli zbliża do 𝑀), to styczna do elipsy składowa siły grawitacji ma ten sam zwrot co wektor prędkości ciała – a zatem prędkość ciała rośnie (położenia ciała na rysunku 1. są coraz rzadziej).
Sposób 2. (Zastosowanie prawa pól Keplera)
Komentarz
Zastosujemy II prawo Keplera (prawo pól).
Zgodnie z II prawem Keplera promień wodzący 𝑟, łączący ciało ze środkiem masy centralnej 𝑀, zakreśla w jednakowych odstępach czasu Δ𝑡 powierzchnie o równych polach Δ𝑆 (zobacz rysunek poniżej).
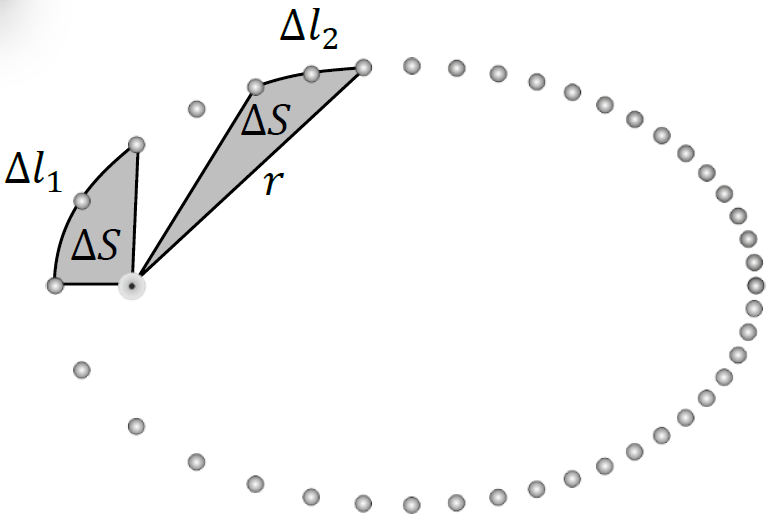
Gdy 𝑟 rośnie, to z równości pól wynika, że ciało zakreśla wzdłuż orbity eliptycznej w jednakowych odstępach czasu coraz mniejsze łuki: Δ𝑙1 > Δ𝑙2. Jeśli więc droga przebyta w jednakowych odstępach czasu maleje, to znaczy, że wartość prędkości ciała maleje. Analogicznie można udowodnić, że wartość prędkości rośnie, gdy 𝑟 maleje.
Sposób 3. (Zastosowanie zasady zachowania energii)
Komentarz
Wykorzystamy zasadę zachowania energii mechanicznej w ruchu ciała jedynie pod wpływem siły grawitacji. W tym celu przeanalizujemy wzór na energię mechaniczną:
𝐸 = 𝐸𝑘𝑖𝑛 + 𝐸𝑝𝑜𝑡 = 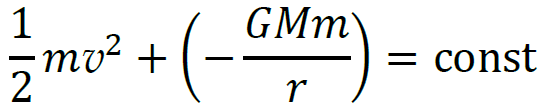
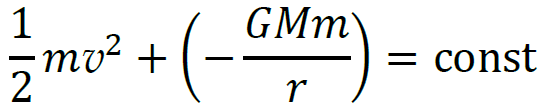
Gdy ciało oddala się od centrum grawitacyjnego (masy 𝑀), to energia potencjalna rośnie (rośnie w zakresie wartości ujemnych). Ponieważ energia mechaniczna musi być zachowana, to przy wzroście energii potencjalnej maleje energia kinetyczna. To z kolei oznacza, że maleje wartość prędkości ciała. Analogicznie dowodzimy wzrostu prędkości, gdy ciało zbliża się do masy 𝑀.
schemat punktacji
2 pkt – poprawne wpisanie odpowiedzi oraz poprawne jej uzasadnienie odwołujące się do
relacji między wielkościami wynikającymi z II zasady dynamiki lub prawa pól Keplera,
lub zasady zachowania momentu pędu, lub zasady zachowania energii.
1 pkt – poprawne wpisanie odpowiedzi oraz brak uzasadniania albo uzasadnienie niepełne.
0 pkt – odpowiedź niepoprawna albo brak odpowiedzi.