Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Zauważmy, że punkt przecięcia osi symetrii funkcji kwadratowej z osią 𝑂𝑥 jest środkiem odcinka, którego końcami są miejsca zerowe tej funkcji. Zatem:
𝑥𝑠 = x1 + x2 ⁄2 zatem 3 = 1 + x2 ⁄2 stąd 𝑥2 = 5
Zapiszemy wzór funkcji 𝑔 w postaci iloczynowej dla pewnego rzeczywistego współczynnika 𝑎:
𝑦 = 𝑔(𝑥) = 𝑎(𝑥 − 1)(𝑥 − 5)
Obliczymy 𝑎. Wykres funkcji przechodzi przez punkt 𝑃 = (2, −6) zatem:
−6 = 𝑎(2 − 1)(2 − 5) czyli − 6 = 𝑎 ⋅ (−3) zatem 𝑎 = 2
Wzór funkcji 𝑦 = 𝑔(𝑥) w postaci iloczynowej ma postać:
𝑦 = 𝑔(𝑥) = 2(𝑥 − 1)(𝑥 − 5)
Sposób 2.
Naszkicujemy fragment wykresu funkcji kwadratowej 𝑦 = 𝑔(𝑥), który spełnia warunki:
1) przechodzi przez punkt 𝑃 = (2, −6),
2) posiada oś symetrii 𝑥 = 3,
3) przecina oś 𝑥 w punkcie (1,0) (miejsce zerowe funkcji 𝑔 to 𝑥1 = 1).
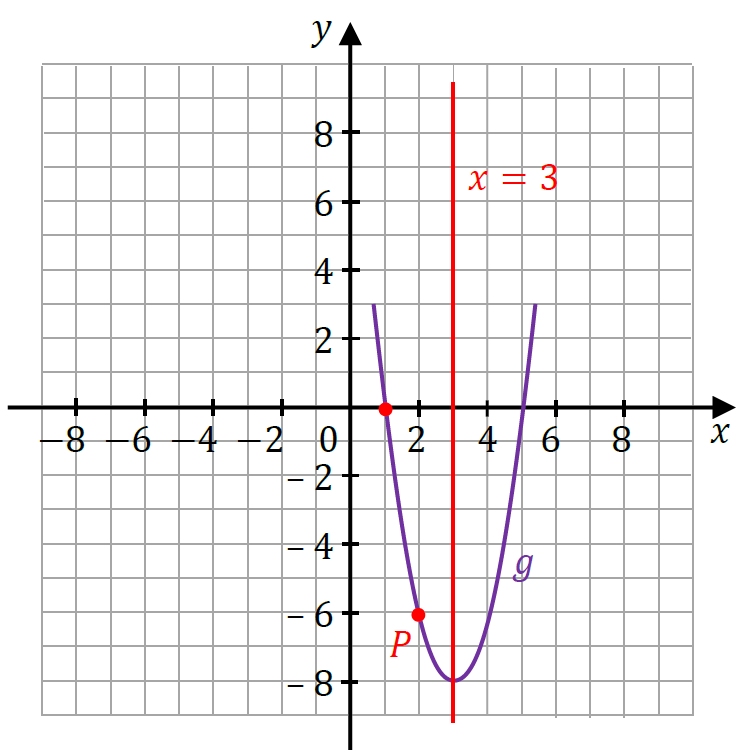
Drugie miejsce zerowe funkcji 𝑔 jest położone symetrycznie do 𝑥1 = 1 względem prostej 𝑥 = 3. Zatem drugim miejscem zerowym jest 𝑥2 = 5. Zapiszemy oba miejsca zerowe:
𝑥1 = 1 𝑥2 = 5
Zapiszemy wzór funkcji 𝑔 w postaci iloczynowej dla pewnego rzeczywistego współczynnika 𝑎:
𝑦 = 𝑔(𝑥) = 𝑎(𝑥 − 1)(𝑥 − 5)
Wyznaczymy 𝑎. Wykres funkcji przechodzi przez punkt 𝑃 = (2, −6), zatem:
−6 = 𝑎(2 − 1)(2 − 5)
Stąd 𝑎 = 2.
Wzór funkcji 𝑦 = 𝑔(𝑥) w postaci iloczynowej ma postać:
𝑦 = 𝑔(𝑥) = 2(𝑥 − 1)(𝑥 − 5)
schemat punktacji
2 pkt – poprawna metoda wyznaczenia postaci iloczynowej funkcji 𝑔 oraz zapisanie jej wzoru: 𝑦 = 𝑔(𝑥) = 2(𝑥 − 1)(𝑥 − 5).
1 pkt – zapisanie wzoru funkcji 𝑔 w postaci 𝑦 = 𝑔(𝑥) = 𝑎(𝑥 − 1)(𝑥 − 5).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.