Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Wysokość maksymalna, na jaką wzniesie się środek piłki, jest równa współrzędnej 𝑦 wierzchołka paraboli. Skorzystamy z gotowego wzoru na wierzchołek paraboli (zobacz w Wybranych wzorach matematycznych):
ℎ𝑚𝑎𝑥 = 𝑦𝑤 =
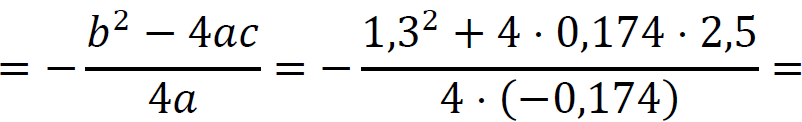
= 4,928 … ≈ 4,93 m
Sposób 2.
Wysokość maksymalna, na jaką wzniesie się środek piłki, jest równa współrzędnej 𝑦 wierzchołka paraboli. Wartość tę możemy wyznaczyć przekształcając wzór funkcji kwadratowej 𝑦 = −0,174𝑥2 + 1,3𝑥 + 2,5 do postaci kanonicznej:
𝑦 = −0,174(𝑥 − 𝑝)2 + 𝑞
gdzie:
ℎ𝑚𝑎𝑥 = 𝑦𝑤 = 𝑞
𝑦 = −0,174𝑥2 + 1,3𝑥 + 2,5 =
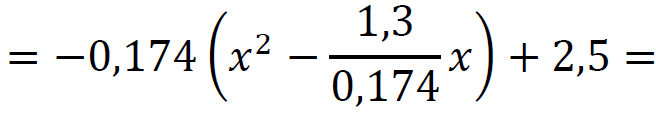
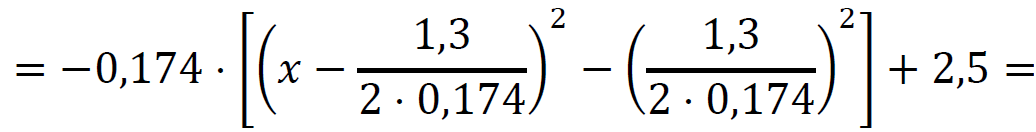
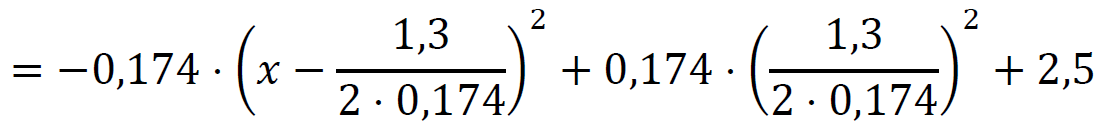
Zatem:
ℎ𝑚𝑎𝑥 = 𝑦𝑤 = 𝑞 =
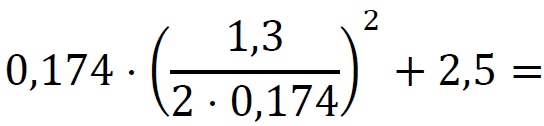
= 4,9281609 … ≈ 4,93 m
schemat punktacji
2 pkt – poprawna metoda rozwiązania oraz zapisanie wyniku 4,93 m.
1 pkt – zastosowanie wzoru na wierzchołek paraboli oraz prawidłowe podstawienie wszystkich danych liczbowych do tego wzoru
LUB
– zapisanie wzoru funkcji w postaci 𝑦 = −0,174(𝑥 − 𝑝)2 + 𝑞 oraz zidentyfikowanie 𝑞
jako współrzędnej wierzchołka paraboli lub wysokości maksymalnej rzutu.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.