Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Wykorzystamy wzór podany we wstępie do zadania, opisujący rozpad promieniotwórczy, zastosowany do masy izotopu:
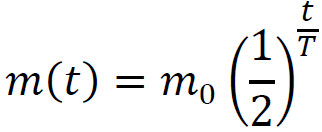
Podstawimy dane z zadania i przekształcimy równanie:
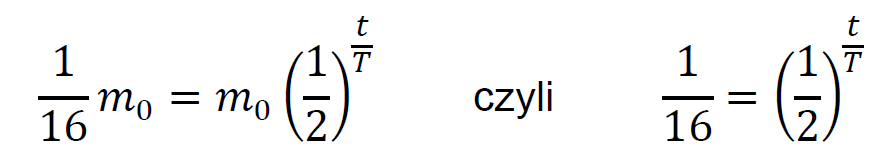
Zgodnie z definicją funkcji wykładniczej, powyższa równość oznacza, że liczba 1⁄2 podniesiona do potęgi t⁄T musi dać w wyniku 1⁄16 . Zatem:
t⁄T = 4
Obliczymy, ile lat liczy sobie znalezisko. Z powyższego równania wynika, że:
𝑡 = 4𝑇 = 4 ⋅ 5700 = 22 800 lat
Sposób 2.
Przyjmijmy, że:
𝑚0 – masa początkowa izotopu węgla 14C
Zgodnie z definicją pojęcia czasu połowicznego rozpadu, po każdym upływie czasu równym czasowi połowicznego rozpadu, masa izotopu promieniotwórczego w próbce zmniejsza się o połowę. Zatem po każdym kolejnym upływie 5700 lat, masa izotopu węgla 14C w próbce/znalezisku będzie się zmniejszała o połowę.
Zatem:
𝑚1 = 1⁄2 ∙ 𝑚0 – masa izotopu węgla 14C w próbce po 5700 latach.
– masa izotopu węgla 14C w próbce po 11400 latach.
– masa izotopu węgla 14C w próbce po 17100 latach.
– masa izotopu węgla 14C w próbce 22800 latach.Znalezisko archeologiczne ma 22800 lat.
schemat punktacji
dla rozwiązania sposobem 1.
3 pkt – poprawna metoda obliczenia 𝑡 oraz podanie prawidłowego wyniku: 𝑡 = 22 800 lat.
2 pkt – zapisanie równania: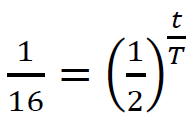 
oraz wyznaczenie z niego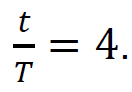 
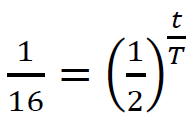oraz wyznaczenie z niego 1 pkt – poprawne zapisanie równania:
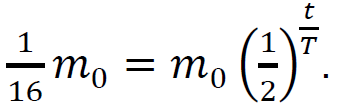
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 2.
3 pkt – poprawna metoda obliczenia, ile lat ma znalezisko archeologiczne oraz podanie prawidłowego wyniku: 22 800 lat.
2 pkt – zapisanie związku między masą izotopu węgla 14C jaka utrzymywała się za życia organizmu a masą tego izotopu w znalezisku: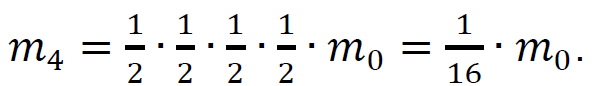 
1 pkt – poprawne zapisanie masy izotopu węgla 14C po 5700 latach (po czasie połowicznego rozpadu): 𝑚1 = 1⁄2 ∙ 𝑚0.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.